题目内容
已知函数f(x)=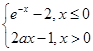 (a是常数且a>0).对于下列命题:
(a是常数且a>0).对于下列命题:
①函数f(x)的最小值是-1;
②函数f(x)在R上是单调函数;
③若f(x)>0在[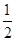 ,+∞)上恒成立,则a的取值范围是a>1;
,+∞)上恒成立,则a的取值范围是a>1;
④对任意x1<0,x2<0且x1≠x2,恒有f(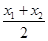 )<
)<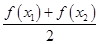 .
.
其中正确命题的所有序号是________.
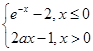 (a是常数且a>0).对于下列命题:
(a是常数且a>0).对于下列命题:①函数f(x)的最小值是-1;
②函数f(x)在R上是单调函数;
③若f(x)>0在[
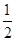 ,+∞)上恒成立,则a的取值范围是a>1;
,+∞)上恒成立,则a的取值范围是a>1;④对任意x1<0,x2<0且x1≠x2,恒有f(
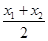 )<
)<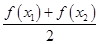 .
.其中正确命题的所有序号是________.
①③④
作出函数f(x)的图象如图所示,显然f(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,所以函数f(x)的最小值为f(0)=-1,故命题①正确;
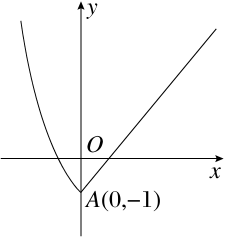
显然,函数f(x)在R上不是单调函数,②错误;
因为f(x)在(0,+∞)上单调递增,故函数f(x)在[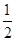 ,+∞)上的最小值为f(
,+∞)上的最小值为f(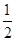 )=2a×
)=2a×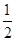 -1=a-1,所以若f(x)>0在[
-1=a-1,所以若f(x)>0在[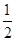 ,+∞)上恒成立,则a-1>0,即a>1,故③正确;
,+∞)上恒成立,则a-1>0,即a>1,故③正确;
由图象可知,在(-∞,0)上,对任意x1<0,x2<0且x1≠x2,恒有f(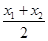 )<
)<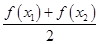 成立,故④正确.
成立,故④正确.
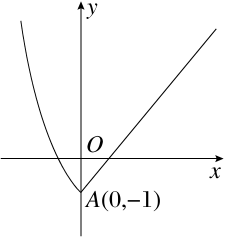
显然,函数f(x)在R上不是单调函数,②错误;
因为f(x)在(0,+∞)上单调递增,故函数f(x)在[
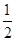 ,+∞)上的最小值为f(
,+∞)上的最小值为f(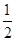 )=2a×
)=2a×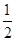 -1=a-1,所以若f(x)>0在[
-1=a-1,所以若f(x)>0在[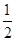 ,+∞)上恒成立,则a-1>0,即a>1,故③正确;
,+∞)上恒成立,则a-1>0,即a>1,故③正确;由图象可知,在(-∞,0)上,对任意x1<0,x2<0且x1≠x2,恒有f(
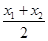 )<
)<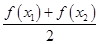 成立,故④正确.
成立,故④正确.
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 的导函数为
的导函数为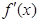 ,当
,当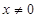 时,
时,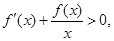 若
若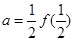 ,
,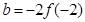 ,
,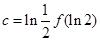 ,则
,则 的大小关系是 .
的大小关系是 .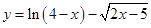 , 则此函数的定义域为 .
, 则此函数的定义域为 .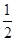 ]
]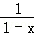 +lg(1+x)的定义域是( )
+lg(1+x)的定义域是( )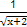 的定义域是( )
的定义域是( )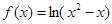 的定义域为( )
的定义域为( )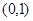
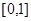
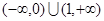
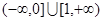
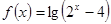 的定义域为________.
的定义域为________.