题目内容
在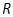 上可导的函数
上可导的函数 的图形如图所示,则关于
的图形如图所示,则关于 的不等式
的不等式 的解集为( ).
的解集为( ).
A. | B. |
C.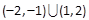 | D. |
A
解析试题分析:由图象可知f′(x)=0的解为x=-1和x=1函数f(x)在(-∞,-1)上增,在(-1,1)上减,在(1,+∞)上增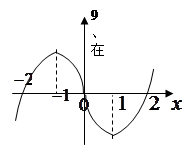
∴f′(x)在(-∞,-1)上大于0,在(-1,1)小于0,在(1,+∞)大于0
当x<0时,f′(x)>0解得x∈(-∞,-1)
当x>0时,f′(x)<0解得x∈(0,1)
综上所述,x∈(-∞,-1)∪(0,1),故选A.
考点:函数的图象;导数的运算;其他不等式的解法.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
定义在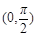 上的函数
上的函数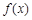 ,
,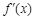 是它的导函数,且恒有
是它的导函数,且恒有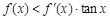 成立,则( )
成立,则( )
A.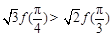 | B.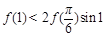 |
C.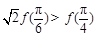 | D.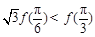 |
已知定义域为R的函数 ,且对任意实数x,总有
,且对任意实数x,总有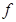 /(x)<3
/(x)<3
则不等式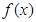 <3x-15的解集为( )
<3x-15的解集为( )
| A.(﹣∞,4) |
| B.(﹣∞,﹣4) |
| C.(﹣∞,﹣4)∪(4,﹢∞) |
| D.(4,﹢∞) |
在区间 内不是增函数的是( )
内不是增函数的是( )
A. | B. |
C. | D. |
定义域为R的函数f(x)满足f(1)=1,且f(x)的导函数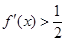 ,则满足
,则满足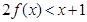 的x的集合为( )
的x的集合为( )
| A.{x|x<1} | B.{x|-1<x<1} | C.{x|x<-1或x>1} | D.{x|x>1} |
曲线 在点(1,1)处切线的斜率等于
在点(1,1)处切线的斜率等于
A. | B.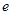 | C.2 | D.1 |
点P是曲线x2-y-2ln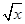 =0上任意一点,则点P到直线4x+4y+1=0的最短距离是( )
=0上任意一点,则点P到直线4x+4y+1=0的最短距离是( )
A.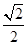 (1-ln 2) (1-ln 2) | B.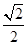 (1+ln 2) (1+ln 2) |
C.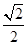 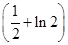 | D.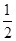 (1+ln 2) (1+ln 2) |
函数f(x)=x2-2ax+a在区间(-∞,1)上有最小值,则函数g(x)=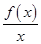 在区间(1,+∞)上一定( )
在区间(1,+∞)上一定( )
| A.有最小值 | B.有最大值 | C.是减函数 | D.是增函数 |
 是
是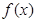 的导函数,
的导函数,