题目内容
已知p:“x2+ y2 +2x=F为一圆的方程(F∈R)”,q:“F>0”,则p是q的
| A.充要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.既不充分也不必要条件 |
C
解析试题分析:“x2+ y2 +2x=F为一圆的方程(F∈R)”,则有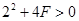 ,即F>-1;反之,若F>0,则
,即F>-1;反之,若F>0,则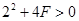 一定成立,所以 ,“x2+ y2 +2x=F为一圆的方程(F∈R)”,故p是q的必要不充分条件,选C。
一定成立,所以 ,“x2+ y2 +2x=F为一圆的方程(F∈R)”,故p是q的必要不充分条件,选C。
考点:本题主要考查充要条件的概念,圆的一般方程。
点评:小综合题,涉及充要条件的判定问题,往往综合性较强,涉及知识面广。充要条件的判定方法有:定义法,等价关系法,集合关系法。

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案
相关题目
下列说法中,正确的是( )
A.命题“若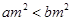 ,则 ,则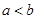 ”的逆命题是真命题 ”的逆命题是真命题 |
B.已知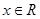 ,则“ ,则“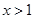 ”是“ ”是“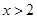 ”的充分不必要条件 ”的充分不必要条件 |
C.命题“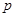 或 或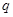 ”为真命题,则命题“ ”为真命题,则命题“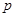 ”和命题“ ”和命题“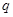 ”均为真命题 ”均为真命题 |
D.命题“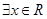 , ,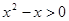 ”的否定是:“ ”的否定是:“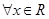 , ,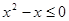 ” ” |
“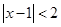 成立”是“
成立”是“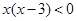 成立”的( )
成立”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
某个命题与正整数n有关,如果当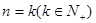 时命题成立,那么可推得当
时命题成立,那么可推得当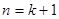 时命题也成立. 现已知当
时命题也成立. 现已知当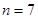 时该命题不成立,那么可推得( )
时该命题不成立,那么可推得( )
| A.当n=6时该命题不成立 | B.当n=6时该命题成立 |
| C.当n=8时该命题不成立 | D.当n=8时该命题成立 |
命题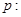
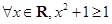 ,则
,则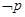 是( )
是( )
A.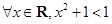 | B.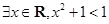 |
C. | D.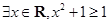 |
设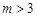 ,对于数列
,对于数列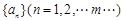 ,令
,令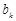 为
为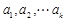 中的最大值,称数列
中的最大值,称数列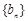 为
为 的“递进上限数列”。例如数列
的“递进上限数列”。例如数列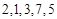 的递进上限数列为2,2,3,7,7.则下面命题中( )
的递进上限数列为2,2,3,7,7.则下面命题中( )
①若数列 满足
满足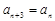 ,则数列
,则数列 的递进上限数列必是常数列
的递进上限数列必是常数列
②等差数列 的递进上限数列一定仍是等差数列
的递进上限数列一定仍是等差数列
③等比数列 的递进上限数列一定仍是等比数列
的递进上限数列一定仍是等比数列
正确命题的个数是( )
| A.0 | B.1 | C.2 | D.3 |
“a=1”是“直线l1:ax+2y-1=0与直线l2:x+(a+1)y+4=0平行”的 ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
已知命题p:3≥3,q:3>4,则下列判断正确的是( )
A.p q为真,p q为真,p q为真, q为真,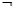 p为假 p为假 | B.p q为真,p q为真,p q为假, q为假,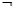 p为真 p为真 |
C.p q为假,p q为假,p q为假, q为假,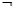 p为假 p为假 | D.p q为真,p q为真,p q为假, q为假,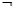 p为假 p为假 |
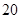 分钟抽取一件产品进行某项指标的检测 ,
分钟抽取一件产品进行某项指标的检测 ,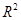 的值越大,说明拟合的效果越好;
的值越大,说明拟合的效果越好;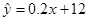 中,当解释变量
中,当解释变量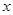 每增加一个单位时,预报变量
每增加一个单位时,预报变量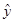 平均增加
平均增加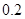 个单位;
个单位; 与
与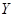 ,若它们的随机变量
,若它们的随机变量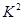 的观测值
的观测值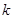 越小,则判断“
越小,则判断“