题目内容
已知f(x)= 在区间[-1,1]上是增函数.
在区间[-1,1]上是增函数.
(Ⅰ)求实数a的值组成的集合A;(Ⅱ)设关于x的方程f(x)= 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.(12分)
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.(12分)
【答案】
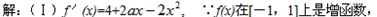
∴f'(x)≥0对x∈[-1,1]恒成立,
即x2-ax-2≤0对x∈[-1,1]恒成立. ①
设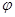 (x)=x2-ax-2,
(x)=x2-ax-2,

设g(t)=m2+tm-2=mt+(m2-2),
g(1)=m2+m-2≥0,
 m≥2或m≤-2.
m≥2或m≤-2.
所以,存在实数m,使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,其取值范围是{m|m≥2,或m≤-2}.
【解析】略

练习册系列答案
相关题目
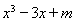
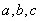
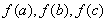
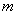
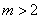
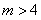
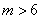
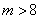
 2x
2x