题目内容
一个三棱锥的三条侧棱两两垂直且长分别为3、4、5,则它的外接球的表面积是( )
分析:先将三棱锥的外接球问题转化为长方体的外接球问题,再利用长方体的对角线计算公式,求得其外接球的直径,进而利用球的表面积计算公式计算即可
解答:解:此三棱锥的外接球即棱长分别为3、4、5的长方体的外接球
而长方体的体对角线即为球的直径
∴球的直径2R=
=5
,∴R=
∴外接球的表面积S=4πR2=4π×
=50π
故选 C
而长方体的体对角线即为球的直径
∴球的直径2R=
| 32+42+52 |
| 2 |
5
| ||
| 2 |
∴外接球的表面积S=4πR2=4π×
| 25 |
| 2 |
故选 C
点评:本题主要考查了球与锥的接切问题,利用三条侧棱两两垂直的三棱锥的外接球即为对应长方体的外接球,可提高效率,减少运算量

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
一个三棱锥的三条侧棱互相垂直,且侧棱长都为2,则此三棱锥的外接球的表面积为( )
| A、4π | B、12π | C、24π | D、48π |
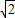 π
π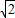 π
π π
π π
π