题目内容
【题目】已知函数f（x）=2sinωxcosωx+2 
sin2ωx﹣ （ω＞0）的最小正周期为π． （Ⅰ）求函数f（x）的单调增区间；
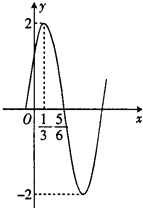
（Ⅱ）将函数f（x）的图象向左平移 
个单位，再向上平移1个单位，得到函数y=g（x）的图象．若y=g（x）在[0，b]（b＞0）上至少含有10个零点，求b的最小值．
【答案】解：（Ⅰ）由题意，可得
f（x）= 
= 
．
∵函数的最小正周期为π，∴ 
=π，解之得ω=1．
由此可得函数的解析式为 
．
令 
，解之得 
∴函数f（x）的单调增区间是 
．
（Ⅱ）将函数f（x）的图象向左平移 
个单位，再向上平移1个单位，可得函数y=f（x+ ）+1的图象，
∵
∴g（x）= 
+1=2sin2x+1，可得y=g（x）的解析式为g（x）=2sin2x+1．
令g（x）=0，得sin2x=﹣ 
，可得2x= 
或2x= 
解之得 
或 
．
∴函数g（x）在每个周期上恰有两个零点，
若y=g（x）在[0，b]上至少含有10个零点，则b不小于第10个零点的横坐标即可，
即b的最小值为 
．
【解析】（I）根据二倍角的三角函数公式与辅助角公式化简得 
，利用周期公式算出ω=1，得函数解析式为 
．再由正弦函数单调区间的公式，解关于x的不等式即可得到函数f（x）的单调增区间；（II）根据函数图象平移的公式，得出函数g（x）的解析式为g（x）=2sin2x+1．由此解g（x）=0得sin2x=﹣ 
，利用正弦函数的图象解出 
或 
，可见g（x）在每个周期上恰有两个零点，若g（x）在[0，b]上至少含有10个零点，则b大于或等于g（x）在原点右侧的第10个零点，由此即可算出b的最小值．
【考点精析】通过灵活运用两角和与差的正弦公式和正弦函数的单调性，掌握两角和与差的正弦公式：
；正弦函数的单调性：在
上是增函数；在
上是减函数即可以解答此题．
