题目内容
18.设f(x)=|2x-1|-|x+1|,(Ⅰ)求f(x)<0的解集;
(Ⅱ)当x<-1时,f(x)>f(a),求实数a的取值范围.
分析 (Ⅰ)画出函数的图象,根据图象求出解集,
(Ⅱ)由图象可知当x<-1时,f(x)>3,继而得到f(a)≤3,解得即可.
解答 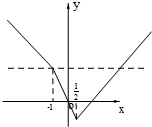 解:(Ⅰ)$f(x)=\left\{{\begin{array}{l}{x-2x≥\frac{1}{2}}\\{-3x-1≤x<\frac{1}{2}}\\{-x+2x<-1}\end{array}}\right.$,其图象如图所示.
解:(Ⅰ)$f(x)=\left\{{\begin{array}{l}{x-2x≥\frac{1}{2}}\\{-3x-1≤x<\frac{1}{2}}\\{-x+2x<-1}\end{array}}\right.$,其图象如图所示.
令f(x)=0解得x1=0,x2=2,
∴f(x)<0的解集为{x|0<x<2},
(Ⅱ)如图,当x<-1时,f(x)>3,
要使f(x)>f(a),
需且只需f(a)≤3,
而f(a)=3时,有-3a=3,或-a+2=3,
即a=-1,或a=5,
得-1≤a≤5.
点评 本题考查了分段函数的图象的画法和应用,以及参数的取值范围,属于中档题.

练习册系列答案
相关题目
9.定积分${∫}_{0}^{2}$(2x+1)dx的值为( )
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
13.曲线y=xex在点(1,e)处的切线与直线ax+by+c=0垂直,则$\frac{a}{b}$的值为( )
| A. | $-\frac{1}{2e}$ | B. | $-\frac{2}{e}$ | C. | $\frac{2}{e}$ | D. | $\frac{1}{2e}$ |
20.cos240°=( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
 如图所示,抛物线C:y2=2px(p>0)与直线AB:y=$\frac{1}{2}$x+b相切于点A.
如图所示,抛物线C:y2=2px(p>0)与直线AB:y=$\frac{1}{2}$x+b相切于点A.