题目内容
已知抛物线y2=2px（p＞0）以椭圆
的右焦点为焦点F．（1）求抛物线方程．
（2）过F做直线L与抛物线交于C，D两点，已知线段CD的中点M横坐标3，求弦|CD|的长度．
【答案】分析：（1）先求出椭圆的右焦点坐标，知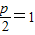
，从而可求得抛物线的标准方程；
（2）由于直线过焦点，先利用中点的坐标公式求出x1+x2，利用弦长公式x1+x2+p求出CD的长．
解答：解：（1）椭圆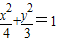
的右焦点（1，0），
由题意知
∴p=2．…（2分）
抛物线的标准方程为y2=4x；
（2）：因为抛物线为y2=4x，
所以p=2
设C、D两点横坐标分别为x1，x2，
因为线段CD中点的横坐标为3，
则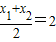
，即x1+x2=6，
故|CD|=x1+x2+p=6+2=8．
点评：本题是直线被圆锥曲线所截，求弦长问题，一般可以由公式：|AB|═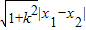
求得；线段中点坐标通常与根与系数的关系相联系，从而简化解题过程．但对于过焦点的弦长注意圆锥曲线定义的应用．
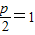，从而可求得抛物线的标准方程；（2）由于直线过焦点，先利用中点的坐标公式求出x1+x2，利用弦长公式x1+x2+p求出CD的长．
解答：解：（1）椭圆
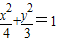的右焦点（1，0），由题意知
∴p=2．…（2分）
抛物线的标准方程为y2=4x；
（2）：因为抛物线为y2=4x，
所以p=2
设C、D两点横坐标分别为x1，x2，
因为线段CD中点的横坐标为3，
则
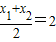，即x1+x2=6，故|CD|=x1+x2+p=6+2=8．
点评：本题是直线被圆锥曲线所截，求弦长问题，一般可以由公式：|AB|═
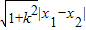求得；线段中点坐标通常与根与系数的关系相联系，从而简化解题过程．但对于过焦点的弦长注意圆锥曲线定义的应用． 
练习册系列答案
相关题目