题目内容
(本题满分12分)若数列 的前n项和为
的前n项和为 ,且有
,且有 ,
,
(1)求 的值;
的值;
(2)求证: ;
;
(3)求出所有满足条件的数列 的通项公式;
的通项公式;
 的前n项和为
的前n项和为 ,且有
,且有 ,
,(1)求
 的值;
的值;(2)求证:
 ;
;(3)求出所有满足条件的数列
 的通项公式;
的通项公式;(1) 或
或 ;(2)见解析;
;(2)见解析;
(3) ;
;
 或
或 ;(2)见解析;
;(2)见解析;(3)
 ;
;本试题主要是考查了数列的前n项和与通项公式的关系式的运用。
(1)n=1入得 或
或
(2)由已知有 ,当
,当 时,有
时,有 ,两式作差得到递推关系式,进而得到结论。
,两式作差得到递推关系式,进而得到结论。
解:(1)n=1入得 或
或 ; …………………2分
; …………………2分
(2)已知有 , ①
, ①
当 时,有
时,有 ②………………………4分
②………………………4分
①-②得: ,即
,即 ; …………6分
; …………6分
(3)由(2)得 或
或 , ………………………7分
, ………………………7分
由 得通项公式为:
得通项公式为: ; …………8分
; …………8分
由 得通项公式为:
得通项公式为: ; …………9分
; …………9分
由 得通项公式为:
得通项公式为: ; …………10分
; …………10分
由 得通项公式为:
得通项公式为: ;…………11分
;…………11分
则所求通项公式为 ;……12分
;……12分
(1)n=1入得
 或
或
(2)由已知有
 ,当
,当 时,有
时,有 ,两式作差得到递推关系式,进而得到结论。
,两式作差得到递推关系式,进而得到结论。解:(1)n=1入得
 或
或 ; …………………2分
; …………………2分(2)已知有
 , ①
, ①当
 时,有
时,有 ②………………………4分
②………………………4分①-②得:
 ,即
,即 ; …………6分
; …………6分(3)由(2)得
 或
或 , ………………………7分
, ………………………7分由
 得通项公式为:
得通项公式为: ; …………8分
; …………8分由
 得通项公式为:
得通项公式为: ; …………9分
; …………9分由
 得通项公式为:
得通项公式为: ; …………10分
; …………10分由
 得通项公式为:
得通项公式为: ;…………11分
;…………11分则所求通项公式为
 ;……12分
;……12分
练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 满足
满足
 .定义:使乘积
.定义:使乘积 …
… 为正整数的
为正整数的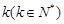 叫做“简易数”.则在
叫做“简易数”.则在 内所有“简易数”的和为 .
内所有“简易数”的和为 . 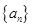 中,
中, 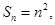 某三角形三边之比为
某三角形三边之比为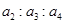 ,则该三角形最大角为
,则该三角形最大角为 
 为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )
为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( ) 的前n项和为
的前n项和为 ,且
,且 , 则
, 则 等于
等于 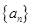 的前
的前 项和
项和 ,而
,而 ,通过计算
,通过计算 ,猜想
,猜想 等于( )
等于( )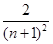


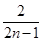
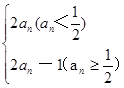 ,若a1=
,若a1=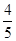 ,则a2012的值为
,则a2012的值为 .
.

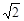 、
、 、
、 、
、 、3
、3 等于( )
等于( )