题目内容
已知a>0且a≠1,若函数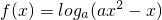 在区间[3,4]上是单调递减函数,则实数a的取值范围为
在区间[3,4]上是单调递减函数,则实数a的取值范围为
- A.

- B.(1,+∞)
- C.
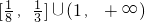
- D.
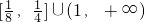
A
分析:令g(x)=ax2-x,则当a>1时,g(x)在[3,4]上单调递减,且g(x)>0,利用二次函数的性质求得实数a的取值范围.当0<a<1时,g(x)在[3,4]上单调递增,且g(x)>0,再利用二次函数的性质求得实数a的取值范围,最后把这两个a的取值范围取并集,即得所求.
解答:令g(x)=ax2-x(a>0,且a≠1),则当a>1时,g(x)在[3,4]上单调递减,且g(x)>0.
∴4≤ ,且 g(4)>0. 解得 a无解.
,且 g(4)>0. 解得 a无解.
则当0<a<1时,g(x)在[3,4]上单调递增,且g(x)>0.
∴ ≤3,且 g(3)>0. 解得 a>
≤3,且 g(3)>0. 解得 a> ,∴1>a>
,∴1>a> .
.
综上可得,实数a的取值范围为 ,
,
故选A.
点评:本题主要考查复合函数的单调性,对数函数的单调性和特殊点,二次函数的性质,体现了分类讨论的数学思想,属中档题.
分析:令g(x)=ax2-x,则当a>1时,g(x)在[3,4]上单调递减,且g(x)>0,利用二次函数的性质求得实数a的取值范围.当0<a<1时,g(x)在[3,4]上单调递增,且g(x)>0,再利用二次函数的性质求得实数a的取值范围,最后把这两个a的取值范围取并集,即得所求.
解答:令g(x)=ax2-x(a>0,且a≠1),则当a>1时,g(x)在[3,4]上单调递减,且g(x)>0.
∴4≤
 ,且 g(4)>0. 解得 a无解.
,且 g(4)>0. 解得 a无解.则当0<a<1时,g(x)在[3,4]上单调递增,且g(x)>0.
∴
 ≤3,且 g(3)>0. 解得 a>
≤3,且 g(3)>0. 解得 a> ,∴1>a>
,∴1>a> .
.综上可得,实数a的取值范围为
 ,
,故选A.
点评:本题主要考查复合函数的单调性,对数函数的单调性和特殊点,二次函数的性质,体现了分类讨论的数学思想,属中档题.

练习册系列答案
相关题目