题目内容
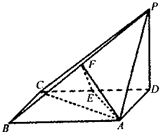
 如图,四棱锥P-ABCD中,底面ABCD为矩形,PD垂直于底面ABCD,AD=PD=2,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PD垂直于底面ABCD,AD=PD=2,
E、F分别为CD、PB的中点.
(1)求证:EF⊥平面PAB;
(2)设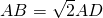 ,求直线AC与平面AEF所成角θ的正弦值.
,求直线AC与平面AEF所成角θ的正弦值.
解:以D为从标原点,DC、DA、DP所在直线分别为x轴、y轴、z轴,建立空间直角坐标系D-xyz.设AB=a,
则A(0,2,0),B(a,2,0),C(a,0,0),D(0,0,0,),p(0,0,2),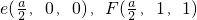 …(2分)
…(2分)
(1)由题意可得: =0×0+1×2+1×(-2)=0,
=0×0+1×2+1×(-2)=0,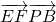 =0×a+1×2+1×(-2)=0
=0×a+1×2+1×(-2)=0
∴EF⊥PA,EF⊥PB.
∴EF⊥平面PAB.…(6分)
(2)AB=2 =(0,1,1).
=(0,1,1).
设平面AEF的法向量n=(x,y,z),
则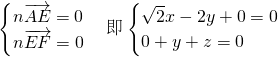
令y=1,则x=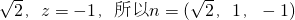 …(9分)
…(9分)
又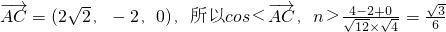 .…(11分)
.…(11分)
所以sinθ=1cos<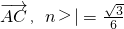 .…(12分)
.…(12分)
分析:(1)求出直线EF所在的向量,再求出平面内两条相交直线所在的向量,然后利用向量的数量积为0,根据线面垂直的判定定理得到线面垂直.
(2)求出平面的法向量以及直线所在的向量,再利用向量的有关运算求出两个向量的夹角,进而转化为线面角,即可解决问题.
点评:解决此类问题的关键是熟练掌握几何体的结构特征,进而得到空间中点、线、面的位置关系,利于建立空间之间坐标系,利用向量的有关知识解决空间角与空间距离以及线面的位置关系等问题.
则A(0,2,0),B(a,2,0),C(a,0,0),D(0,0,0,),p(0,0,2),
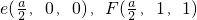 …(2分)
…(2分)
(1)由题意可得:
 =0×0+1×2+1×(-2)=0,
=0×0+1×2+1×(-2)=0,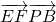 =0×a+1×2+1×(-2)=0
=0×a+1×2+1×(-2)=0∴EF⊥PA,EF⊥PB.
∴EF⊥平面PAB.…(6分)
(2)AB=2
 =(0,1,1).
=(0,1,1).设平面AEF的法向量n=(x,y,z),
则
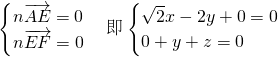
令y=1,则x=
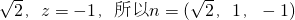 …(9分)
…(9分)又
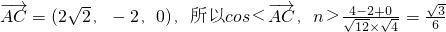 .…(11分)
.…(11分)所以sinθ=1cos<
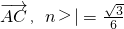 .…(12分)
.…(12分)分析:(1)求出直线EF所在的向量,再求出平面内两条相交直线所在的向量,然后利用向量的数量积为0,根据线面垂直的判定定理得到线面垂直.
(2)求出平面的法向量以及直线所在的向量,再利用向量的有关运算求出两个向量的夹角,进而转化为线面角,即可解决问题.
点评:解决此类问题的关键是熟练掌握几何体的结构特征,进而得到空间中点、线、面的位置关系,利于建立空间之间坐标系,利用向量的有关知识解决空间角与空间距离以及线面的位置关系等问题.

练习册系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=