题目内容
下列函数中既是增函数又是奇函数的是
A.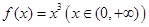 | B.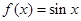 |
C.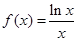 | D.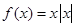 |
D
解析试题分析:四个选项中都给出了具体的函数解析式,其中选项D是分段函数,可由f(-x)=-x|-x|=-x|x|=-f(x)知函数为奇函数,在分析x>0时函数的增减性,根据奇函数的对称性进一步得到函数在整个定义域内的增减性;选项B举一反例即可; C、A中的两个函数,定义域均不关于原点对称,都不是奇函数.根据题意,由于解:由f(-x)=-x|-x|=-x|x|=-f(x),知函数f(x)=x|x|为奇函数,又f(x)=x|x|= x2 (x>0),-x2 (x<0)
当x>0时,f(x)=x2在(0,∞)上为增函数,根据奇函数图象关于原点中心对称,所以当x<0时,f(x)=-x2在(-∞,0)上也为增函数,所以函数f(x)=x|x|在定义域内既是奇函数,又是增函数,故A正确.由于正弦函数是周期性函数,不满足定义域内增函数,因此错误,对于C,A,定义域部关于原点对称,故选D.
考点:函数的奇偶性及函数的单调性
点评:本题主要考查了函数的奇偶性及函数的单调性的判断,尤其y=tanx的单调区间是解答中容易出现错误的地方,要注意掌握.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
方程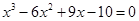 的实根个数是( )
的实根个数是( )
| A.3 | B.2 | C.1 | D.0 |
与函数y=|x|有相同图像的一个函数是( )
A.y= | B.y=a | C.y= | D.y=log5x |
函数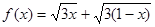 的最大值为
的最大值为
A.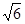 | B.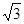 | C.3 | D.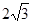 |
已知 , 四个函数中,当
, 四个函数中,当 时, 满足不等式
时, 满足不等式 的是
的是
A. | B. |
C. | D. |
定义域为R的函数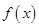 满足
满足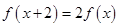 ,当
,当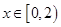 时,
时,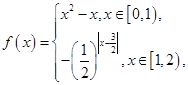 则当
则当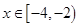 时,函数
时,函数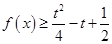 恒成立,则实数
恒成立,则实数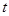 的取值范围为( )
的取值范围为( )
A.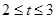 | B.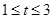 | C.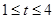 | D.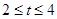 |
下列函数中,在 上为增函数的是 ( )
上为增函数的是 ( )
A. | B. | C. | D. |
已知直线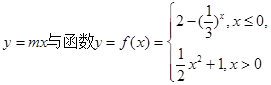 的图象恰好有3个不同的公共点,则实数m的取值范围是( )
的图象恰好有3个不同的公共点,则实数m的取值范围是( )
A.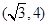 | B.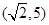 | C. | D. |
下列函数中,与函数y= 定义域相同的函数为( )
定义域相同的函数为( )
A.y= | B.y= | C.y=xex | D.y= |