题目内容
定义域为R的函数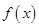 满足
满足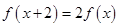 ,当
,当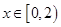 时,
时,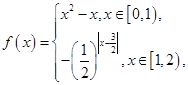 则当
则当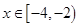 时,函数
时,函数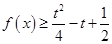 恒成立,则实数
恒成立,则实数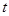 的取值范围为( )
的取值范围为( )
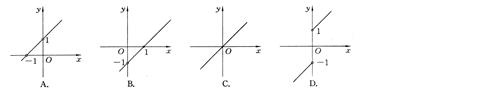
A.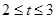 | B.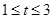 | C.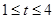 | D.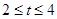 |
B
解析试题分析:解:当x∈[0,1)时,f(x)=x2-x∈[-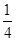 ,0],当x∈[1,2)时,f(x)=-(0.5)|x-1.5|∈[-1,-
,0],当x∈[1,2)时,f(x)=-(0.5)|x-1.5|∈[-1,- ],∴当x∈[0,2)时,f(x)的最小值为-1,又∵函数f(x)满足f(x+2)=2f(x),当x∈[-2,0)时,f(x)的最小值为-
],∴当x∈[0,2)时,f(x)的最小值为-1,又∵函数f(x)满足f(x+2)=2f(x),当x∈[-2,0)时,f(x)的最小值为- ,当x∈[-4,-2)时,f(x)的最小值为-
,当x∈[-4,-2)时,f(x)的最小值为-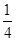 ,若x∈[-4,-2]时,f(x)≥
,若x∈[-4,-2]时,f(x)≥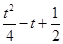
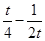 -恒成立,∴
-恒成立,∴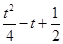 ≤-
≤-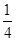 ,解得:t∈[1,3],故选B
,解得:t∈[1,3],故选B
考点:函数恒成立问题
点评:本题考查的知识点是函数恒成立问题,函数的最值,分式不等式的解法,高次不等式的解法,是函数、不等式的综合应用,难度较大.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
已知f(x)是以2为周期的偶函数,当x∈[0, 1]时,f(x)=x,那么在区间[-1,3]内关于x的方程f(x)=kx+k+1(k∈R,k≠-1)的根的个数
| A.不可能有3个 | B.最少有1个,最多有4个 |
| C.最少有1个,最多有3个 | D.最少有2个,最多有4个 |
函数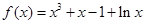 的零点所在的大致区间为
的零点所在的大致区间为
A.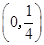 | B.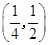 |
C.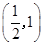 | D.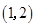 |
下列函数中既是增函数又是奇函数的是
A.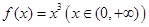 | B.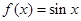 |
C.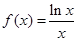 | D.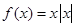 |
下列函数中,既是偶函数又在 单调递增的函数是 ( )
单调递增的函数是 ( )
A. | B. | C. | D. |
已知定义在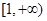 上的函数
上的函数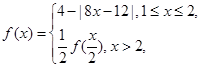 则
则
A.函数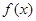 的值域为 的值域为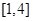 |
B.关于x的方程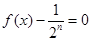 ( (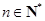 )有4个不相等的实数根 )有4个不相等的实数根 |
C.存在实数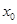 ,使得不等式 ,使得不等式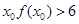 成立 成立 |
D.当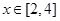 时,函数 时,函数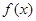 的图象与x轴围成的面积为1 的图象与x轴围成的面积为1 |
函数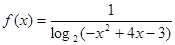 的定义域为( )
的定义域为( )
| A.(1,2)∪(2,3) | B.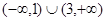 |
| C.(1,3) | D.[1,3] |
下列函数在其定义域内,既是奇函数又存在零点的是: ( )
A. | B.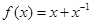 | C.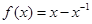 | D.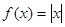 |
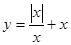 的图象是( )
的图象是( )