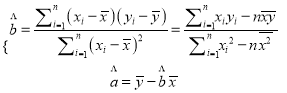题目内容
【题目】若无穷数列![]() 满足:
满足: ![]() ,对于
,对于![]() ,都有
,都有![]() (其中
(其中![]() 为常数),则称
为常数),则称![]() 具有性质“
具有性质“![]() ”.
”.
(Ⅰ)若![]() 具有性质“
具有性质“![]() ”,且
”,且![]() ,
, ![]() ,
, ![]() ,求
,求![]() ;
;
(Ⅱ)若无穷数列![]() 是等差数列,无穷数列
是等差数列,无穷数列![]() 是公比为正数的等比数列,
是公比为正数的等比数列, ![]() ,
, ![]() ,
, ![]() ,判断
,判断![]() 是否具有性质“
是否具有性质“![]() ”,并说明理由;
”,并说明理由;
(Ⅲ)设![]() 既具有性质“
既具有性质“![]() ”,又具有性质“
”,又具有性质“![]() ”,其中
”,其中![]() ,
, ![]() ,
, ![]() 互质,求证:
互质,求证: ![]() 具有性质“
具有性质“![]() ”.
”.
【答案】(1)![]() ,
, ![]() (2)见解析(3见解析)
(2)见解析(3见解析)
【解析】试题分析: (1)因为![]() 具有性质“
具有性质“![]() ”,所以
”,所以![]() ,
, ![]() .再根据已知数据,求出
.再根据已知数据,求出![]() 即可; (2)设等差数列
即可; (2)设等差数列![]() 的公差为
的公差为![]() ,由
,由 ![]() ,
, ![]() ,故
,故![]() . 设等比数列
. 设等比数列![]() 的公比为
的公比为![]() ,由
,由 ![]() ,
, ![]() ,故
,故![]() ,所以
,所以![]() . 若
. 若![]() 具有性质“
具有性质“![]() ”,则
”,则![]() ,
, ![]() .又
.又![]() ,故
,故![]() 不具有性质“
不具有性质“![]() ”;(3) 因为
”;(3) 因为![]() 具有性质“
具有性质“![]() ”,所以
”,所以![]() ,
, ![]() .①
.①
因为![]() 具有性质“
具有性质“![]() ”,所以
”,所以![]() ,
, ![]() .②,化简整理得
.②,化简整理得![]() ,
, ![]() ,得证.
,得证.
试题解析:解 :(Ⅰ)因为![]() 具有性质“
具有性质“![]() ”,所以
”,所以![]() ,
, ![]() .
.
由![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() .
.
因为![]() ,所以
,所以![]() ,即
,即![]() .
.
(Ⅱ)![]() 不具有性质“
不具有性质“![]() ”.
”.
设等差数列![]() 的公差为
的公差为![]() ,由
,由 ![]() ,
, ![]() ,
,
得![]() ,所以
,所以![]() ,故
,故![]() .
.
设等比数列![]() 的公比为
的公比为![]() ,由
,由 ![]() ,
, ![]() ,
,
得![]() ,又
,又![]() ,所以
,所以![]() ,故
,故![]() ,
,
所以![]() .
.
若![]() 具有性质“
具有性质“![]() ”,则
”,则![]() ,
, ![]() .
.
因为![]() ,
, ![]() ,所以
,所以![]() ,
,
故![]() 不具有性质“
不具有性质“![]() ”.
”.
(Ⅲ)因为![]() 具有性质“
具有性质“![]() ”,所以
”,所以![]() ,
, ![]() .①
.①
因为![]() 具有性质“
具有性质“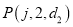 ”,所以
”,所以![]() ,
, ![]() .②
.②
因为![]() ,
, ![]() ,
, ![]() 互质,
互质,
所以由①得![]() ;由②,得
;由②,得![]() ,
,
所以![]() ,即
,即![]() .
.
②-①,得![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,
,
所以![]() 具有性质“
具有性质“![]() ”.
”.

练习册系列答案
相关题目
【题目】在国家“大众创业,万众创新”战略下,某企业决定加大对某种产品的研发投入,已知研发投入![]() (十万元)与利润
(十万元)与利润![]() (百万元)之间有如下对应数据:
(百万元)之间有如下对应数据:
| 2 | 3 | 4 | 5 | 6 |
| 2 | 4 | 5 | 6 | 7 |
若由资料知![]() 对
对![]() 呈线性相关关系。试求:
呈线性相关关系。试求:
(1)线性回归方程![]() ;
;
(2)估计![]() 时,利润是多少?
时,利润是多少?
附:利用“最小二乘法”计算a,b的值时,可根据以下公式: