题目内容
设圆满足:(1)截y轴所得弦长为2;(2)被x轴分成两段圆弧,其弧长的比为3∶1.在满足(1)(2)的所有圆中,求圆心到l∶x-2y=0的距离最小的圆的方程.
答案:略
解析:
解析:
|
设圆的圆心 P(a,b),半径为r,则点P到x轴,y轴的距离分别为|b|,|a|.由题设知圆 P被x轴截得的劣弧所对的圆心角为90°,故圆 P截x轴所得的弦长为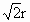
∴ 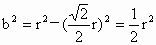 , ,
∵圆 P截y轴所得的弦长为2,∴ 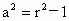 . .
以上两式联立,消去 r,得: 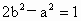 . .
∵点 P(a,b)到直线l的距离为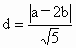 , ,
∴ 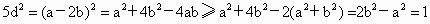 , ,
当且仅当 a=b时上式等号成立,此时 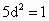 ,从而d取得最小值, ,从而d取得最小值,
由此有 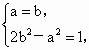 , ,
解得 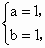 或 或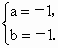
由 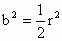 得: 得: , ,
∴符合题意的圆的方程为 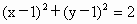 或 或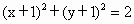 . . |

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目