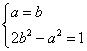Question

设圆满足：(1)截y轴所得弦长为2；(2)被x轴分成两段圆弧，其弧长的比为3∶1，在满足条件(1)、(2)的所有圆中，求圆心到直线l：x－2y=0的距离最小的圆的方程.

 

Answer 1

答案：
解析：

设圆的圆心为P（a，b）半径为r，则点P到x轴，y轴的距离分别为. 由题设知圆P截x轴所得劣弧对的圆心角为90º，知圆P截x轴所得的弦长为r，故r2=2b2.又圆截y轴所得的弦长为2，所以有r2=a2+1，从而得2b2－a2=1. ∵点P(a，b)到直线x－2y=0的距离为 ∴   当且仅当a=b时上式等号成立，此时5d2=1，从而d取最小值，   由此有，   解此方程组得   由于r2=2b2知r=，   于是，所求圆的方程是 (x－1)2+(y－1)2=2或(x+1)2+(y－1)2=2.