题目内容
【题目】已知公比不等于1的等比数列{an},满足:a3=3,S3=9,其中Sn为数列{an}的前n项和.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=log2![]() , 若cn=
, 若cn=![]() , 求数列{cn}的前n项和Tn .
, 求数列{cn}的前n项和Tn .
【答案】解:(Ⅰ)设数列{an}的公比为q,
则有3(1+![]() +
+![]() )=9,
)=9,
解得,q=1(舍去)或q=﹣![]() ,
,
故an=3(﹣![]() )n﹣3;
)n﹣3;
(Ⅱ)a2n+3=3![]() ,
,
故bn=log2![]() =2n,
=2n,
故cn=![]() =
=![]() =
=![]() ﹣
﹣![]() ,
,
故Tn=1﹣![]() +
+![]() ﹣
﹣![]() +…+
+…+![]() ﹣
﹣![]()
=1﹣![]() =
=![]() .
.
【解析】(Ⅰ)设数列{an}的公比为q,从而得方程3(1+![]() +
+![]() )=9,从而解得;
)=9,从而解得;
(Ⅱ)化简a2n+3=3![]() , 从而可得cn=
, 从而可得cn=![]() =
=![]() =
=![]() ﹣
﹣![]() , 从而求和.
, 从而求和.
【考点精析】解答此题的关键在于理解等比数列的通项公式(及其变式)的相关知识,掌握通项公式:![]() ,以及对数列的前n项和的理解,了解数列{an}的前n项和sn与通项an的关系
,以及对数列的前n项和的理解,了解数列{an}的前n项和sn与通项an的关系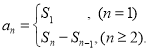 .
.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目