题目内容
【题目】已知圆C过点![]() ,且与圆
,且与圆![]() 外切于点
外切于点![]() ,
,![]() 是x轴上的一个动点.
是x轴上的一个动点.
![]() 求圆C的标准方程;
求圆C的标准方程;
![]() 当圆C上存在点Q,使
当圆C上存在点Q,使![]() ,求实数m的取值范围;
,求实数m的取值范围;
![]() 当
当![]() 时,过P作直线PA,PB与圆C分别交于异于点P的点A,B两点,且
时,过P作直线PA,PB与圆C分别交于异于点P的点A,B两点,且![]() 求证:直线AB恒过定点.
求证:直线AB恒过定点.
【答案】(1)![]() (2)
(2)![]() (3)直线AB恒过定点
(3)直线AB恒过定点![]() .
.
【解析】
1)设出圆的标准方程x2+(y﹣b)2=r2,由已知可得关于r,b的方程组求解得答案;
(2)把圆C上存在点Q,使∠CPQ=30°,转化为直线y=![]() (x﹣m)与圆C有交点,由圆心到直线的距离小于半径求解;
(x﹣m)与圆C有交点,由圆心到直线的距离小于半径求解;
(3)m=1时,P(1,0),设kPA=k,则kPB=![]() ,可得直线PA,PB的方程,与圆的方程联立,求得A,B的坐标,写出AB所在直线方程,分别取k=1和﹣1,得到直线方程,联立求得交点坐标,再代回直线方程验证得答案.
,可得直线PA,PB的方程,与圆的方程联立,求得A,B的坐标,写出AB所在直线方程,分别取k=1和﹣1,得到直线方程,联立求得交点坐标,再代回直线方程验证得答案.
![]() 设圆C:
设圆C:![]() ,
,
则![]() ,解得,
,解得,![]() ,
,![]() ,
,
故圆C的标准方程为:![]() ;
;
![]() 解:当圆C上存在点Q,使
解:当圆C上存在点Q,使![]() ,等价于直线
,等价于直线![]() 与圆C有交点,
与圆C有交点,
![]() 圆C到直线
圆C到直线![]() 的距离小于等于半径1,
的距离小于等于半径1,
即![]() ,解得
,解得![]() ,
,
故实数m的取值范围是![]() ;
;
![]() 证明:
证明:![]() 时,
时,![]() ,设
,设![]() ,则
,则![]() ,
,
则直线PA:![]() ,PB:
,PB:![]() ,
,
联立![]() ,得
,得![]() ,
,
则![]() ,得
,得![]() ,
,![]() .
.
![]() ,
,
同理可得![]()
则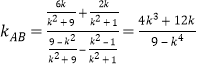 .
.
![]() 直线AB的方程为
直线AB的方程为![]()
当![]() 时,直线方程为
时,直线方程为![]() ,当
,当![]() 时,直线方程为
时,直线方程为![]() .
.
联立![]() ,解得
,解得![]() ,
,![]() .
.
把点![]() 代入
代入![]() 成立,
成立,
![]() 直线AB恒过定点
直线AB恒过定点![]() .
.

练习册系列答案
相关题目


