题目内容
（1）若四边形ABCD的对角线AC将四边形分成面积相等的两个三角形，证明直线AC必平分对角线BD．
（2）写出（1）的逆命题，这个逆命题是否正确？为什么？
（2）写出（1）的逆命题，这个逆命题是否正确？为什么？
（1）证：S△ABC=S△ADC′
且△ABC与△ADC有同底AC，
∴两高线相等：BE=DF
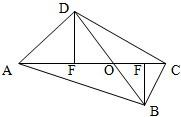
设AC与BD交于点O，
则Rt△BOE≌Rt△DOF，∴OB=OD，即AC平分BD．
（2）逆命题：若四边形ABCD的对角线AC平分对角线BD，
则AC必将四边形分成两个面积相等的三角形这个逆命题是正确的．
证明如下：在图中，由于OB=OD，∠BOE=∠DOF
，∠BEO=∠DFO=Rt∠，∴△BOE≌△DOF．
∴BE=DF，即两高线相等．∴S△ABC=
AC?BE=
AC?DF=S△ADC'．
且△ABC与△ADC有同底AC，
∴两高线相等：BE=DF
设AC与BD交于点O，
则Rt△BOE≌Rt△DOF，∴OB=OD，即AC平分BD．
（2）逆命题：若四边形ABCD的对角线AC平分对角线BD，
则AC必将四边形分成两个面积相等的三角形这个逆命题是正确的．
证明如下：在图中，由于OB=OD，∠BOE=∠DOF
，∠BEO=∠DFO=Rt∠，∴△BOE≌△DOF．
∴BE=DF，即两高线相等．∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
练习册系列答案
暑假作业海燕出版社系列答案
相关题目
设△ABC的外心为O，以线段OA、OB为邻边作平行四边形，第四个顶点为D，再以OC、OD为邻边作平行四边形，它的第四个顶点为H．
在三棱柱ABC-A1B1C1中，∠ACB=120°，AC=CB=1，D1是线段A1B1上一动点（可以与A1或B1重合）．过D1和CC1的平面与AB交于D．
，AC=CB=1，D1是线段A1B1上一动点（可以与A1或B1重合）。过D1和CC1的平面与AB交于D。
