题目内容
(本题满分12分)
在三棱柱ABC-A1B1C1中,∠ACB= ,AC=CB=1,D1是线段A1B1上一动点(可以与A1或B1重合)。过D1和CC1的平面与AB交于D。
,AC=CB=1,D1是线段A1B1上一动点(可以与A1或B1重合)。过D1和CC1的平面与AB交于D。
(1)若四边形CDD1C1总是矩形,求证:三棱柱ABC-A1B1C1为直三棱柱;
(2)在(1)的条件下,求二面角B-AD1-C的取值范围。

【答案】
解:(1)略…………………………5分;
(2)建立如图所示的直角坐标系,则A(0,- ,0),C(,0,0),
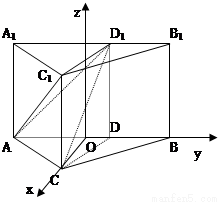
设D(0,a,0),则D1(0,a,1),a∈[- ,],
显然平面BAD1的一个法向量为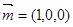 ,可以求出平面ACD1的一个设D(0,a,0),则D1(0,a,1),a∈[- ,],
,可以求出平面ACD1的一个设D(0,a,0),则D1(0,a,1),a∈[- ,],
显然平面BAD1的一个法向量为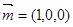 ,可以求出平面ACD1的一个法向量
,可以求出平面ACD1的一个法向量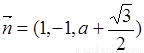 ,于是
,于是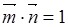 ,
,
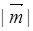 2=2+(a+)2∈[2,5], cosθ∈[,],
2=2+(a+)2∈[2,5], cosθ∈[,],
所以θ∈[arccos,]………………………………12分
【解析】略

练习册系列答案
相关题目
 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面