题目内容
已知曲线C的方程为kx2+(4-k)y2=k+1(k∈R).
(1)若曲线C是椭圆,求k的取值范围;
(2)若曲线C是双曲线,且有一条渐近线的倾斜角是60°,求此双曲线的方程;
(3)满足(2)的双曲线上是否存在两点P、Q关于直线l:y=x-1对称,若存在,求出过P、Q的直线方程;若不存在,说明理由.
解:(1)当k=0或k=-1或k=4时,C表示直线;
当k≠0且k≠-1且k≠4时方程为
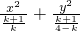 =1,①
=1,①
方程①表示椭圆的充要条件是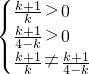
即是0<k<2或2<k<4.
(2)方程①表示双曲线的充要条件是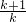 •
•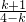 <0,
<0,
即k<-1或-1<k<0或k>4.
①当k<-1或k>4时,双曲线焦点在x轴上,
a2=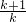 ,b2=
,b2=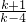 ,
,
其一条渐近线的斜率为 =
=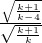 =
= ,得k=6.
,得k=6.
②当-1<k<0时,双曲线焦点在y轴上,
a2=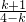 ,b2=-
,b2=-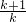 ,
,
其一条渐近线的斜率为 =
=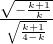 =
= ,得k=6(舍),
,得k=6(舍),
综上得双曲线方程为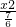 -
-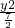 =1.
=1.
(3)若存在,设直线PQ的方程为:y=-x+m.
由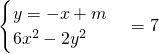 ,
,
消去y,
得4x2+4mx-2m2-7=0.②
设P、Q的中点是M(x0,y0),则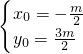
M在直线l上,
∴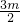 =-
=- -1,解得m=-
-1,解得m=- ,方程②的△>0,
,方程②的△>0,
∴存在满足条件的P、Q,直线PQ的方程为y=-x- .
.
分析:(1)当k=0或k=-1或k=4时,C表示直线;当k≠0且k≠-1且k≠4时方程为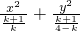 =1,由此能求出若曲线C是椭圆,k的取值范围.
=1,由此能求出若曲线C是椭圆,k的取值范围.
(2)曲线C是双曲线的充要条件是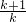 •
•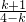 <0,即k<-1或-1<k<0或k>4.再由有一条渐近线的倾斜角是60°,能求出双曲线方程.
<0,即k<-1或-1<k<0或k>4.再由有一条渐近线的倾斜角是60°,能求出双曲线方程.
(3)若存在,设直线PQ的方程为:y=-x+m.由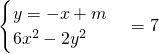 ,得4x2+4mx-2m2-7=0.由此能推导出存在满足条件的P、Q,直线PQ的方程为y=-x-
,得4x2+4mx-2m2-7=0.由此能推导出存在满足条件的P、Q,直线PQ的方程为y=-x- .
.
点评:本题考查直线与圆锥曲线的综合运用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答.
当k≠0且k≠-1且k≠4时方程为
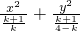 =1,①
=1,①方程①表示椭圆的充要条件是
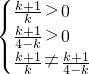
即是0<k<2或2<k<4.
(2)方程①表示双曲线的充要条件是
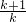 •
•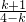 <0,
<0,即k<-1或-1<k<0或k>4.
①当k<-1或k>4时,双曲线焦点在x轴上,
a2=
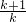 ,b2=
,b2=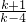 ,
,其一条渐近线的斜率为
 =
=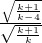 =
= ,得k=6.
,得k=6.②当-1<k<0时,双曲线焦点在y轴上,
a2=
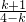 ,b2=-
,b2=-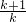 ,
,其一条渐近线的斜率为
 =
=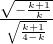 =
= ,得k=6(舍),
,得k=6(舍),综上得双曲线方程为
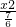 -
-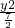 =1.
=1.(3)若存在,设直线PQ的方程为:y=-x+m.
由
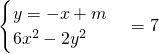 ,
,消去y,
得4x2+4mx-2m2-7=0.②
设P、Q的中点是M(x0,y0),则
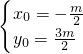
M在直线l上,
∴
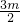 =-
=- -1,解得m=-
-1,解得m=- ,方程②的△>0,
,方程②的△>0,∴存在满足条件的P、Q,直线PQ的方程为y=-x-
 .
.分析:(1)当k=0或k=-1或k=4时,C表示直线;当k≠0且k≠-1且k≠4时方程为
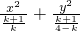 =1,由此能求出若曲线C是椭圆,k的取值范围.
=1,由此能求出若曲线C是椭圆,k的取值范围.(2)曲线C是双曲线的充要条件是
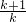 •
•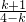 <0,即k<-1或-1<k<0或k>4.再由有一条渐近线的倾斜角是60°,能求出双曲线方程.
<0,即k<-1或-1<k<0或k>4.再由有一条渐近线的倾斜角是60°,能求出双曲线方程.(3)若存在,设直线PQ的方程为:y=-x+m.由
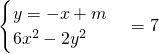 ,得4x2+4mx-2m2-7=0.由此能推导出存在满足条件的P、Q,直线PQ的方程为y=-x-
,得4x2+4mx-2m2-7=0.由此能推导出存在满足条件的P、Q,直线PQ的方程为y=-x- .
.点评:本题考查直线与圆锥曲线的综合运用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目