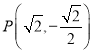题目内容
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,
,![]() 是椭圆上关于原点
是椭圆上关于原点![]() 对称的两个动点,当点
对称的两个动点,当点![]() 的坐标为
的坐标为![]() 时,
时,![]() 的周长恰为
的周长恰为![]() .
.
(1)求椭圆的方程;
(2)过点![]() 作直线
作直线![]() 交椭圆于
交椭圆于![]() 两点,且
两点,且![]()
![]() ,求
,求![]() 面积的取值范围.
面积的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)求出AB,得到a,然后求解b,即可得到椭圆方程;(2)当直线AB的斜率不存在时,求解三角形面积,设直线CD的方程为y=k(x+2)(k≠0).由![]() 消去y整理得:(1+2k2)x2+8k2x+8k2﹣8=0,△>0,设C(x1,y1),D(x2,y2),利用弦长公式求解CD,然后求解三角形面积,推出范围即可.
消去y整理得:(1+2k2)x2+8k2x+8k2﹣8=0,△>0,设C(x1,y1),D(x2,y2),利用弦长公式求解CD,然后求解三角形面积,推出范围即可.
(1)当点![]() 的坐标为
的坐标为![]() 时,
时,![]() ,所以
,所以![]() .
.
由对称性,![]() ,
,
所以![]() ,得
,得![]()
将点![]() 代入椭圆方程
代入椭圆方程![]() 中,解得
中,解得![]() ,
,
所以椭圆方程为![]() .
.
(2)当直线![]() 的斜率不存在时,
的斜率不存在时,![]() ,
,
此时![]() .
.
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() .
.
由![]() 消去
消去![]() 整理得:
整理得:![]() . 显然
. 显然![]() ,
,
设![]() ,则
,则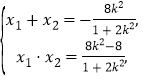
故![]()

![]()
![]() .
.
因为![]()
![]() ,所以
,所以![]() ,
,
所以点![]() 到直线
到直线![]() 的距离即为点
的距离即为点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
所以![]()
![]()
![]()
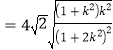
![]()
![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() .综上,
.综上,![]() .
.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案【题目】为了了解高一学生的心理健康状况,某校心理健康咨询中心对该校高一学生的睡眠状况进行了抽样调查.该中心随机抽取了60名高一男生和40名高一女生,统计了他们入学第一个月的平均每天睡眠时间,得到如下频数分布表.规定:“平均每天睡眠时间大于等于8小时”为“睡眠充足”,“平均每天睡眠时间小于8小时”为“睡眠不足”.
高一男生平均每天睡眠时间频数分布表
睡眠时间(小时) |
|
|
|
|
|
频数 | 3 | 20 | 19 | 10 | 8 |
高一女生平均每天睡眠时间频数分布表
睡眠时间(小时) |
|
|
|
|
|
频数 | 20 | 11 | 5 | 2 |
(1)请将下面的列联表补充完整,并根据已完成的![]() 列联表,判断是否有
列联表,判断是否有![]() 的把握认为“睡眠是否充足与性别有关”?
的把握认为“睡眠是否充足与性别有关”?
睡眠充足 | 睡眠不足 | 合计 | |
男生 | 42 | ||
女生 | 7 | ||
合计 | 100 |
(2)由样本估计总体的思想,根据这两个频数分布表估计该校全体高一学生入学第一个月的平均每天睡眠时间(同一组中的数据以这组数据所在区间中点的值作代表);
(3)若再从这100人中平均每天睡眠时间不足6小时的同学里随机抽取两人进行心理健康干预,则抽取的两人中包含女生的概率是多少?
附:参考公式:![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |