题目内容
(本小题满分13分)如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD^底面ABCD,PD=DC,点E是PC的中点,作EF^PB交PB于点F,
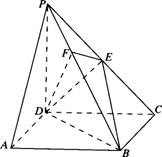
(1)求证:PA//平面EDB;
(2)求证:PB^平面EFD;
(3)求二面角C-PB-D的大小。
【答案】
解:如右图所示建立空间直角坐标系,点D为坐标原点,设DC=1。
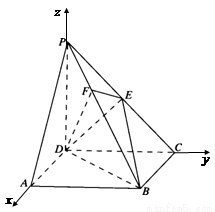
(1)证明:连结AC, AC交BD于点G,连结EG.
依题意得A(1,0,0),P(0,0,1),E(0,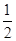 ,
,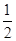 ).
).
因为底面ABCD是正方形,所以点G是此正
方形的中心,故点G的坐标为(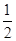 ,
,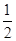 ,0),
,0),
且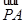 =(1,0,-1),
=(1,0,-1),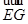 =(
=(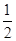 ,0,-
,0,- 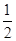 ).
).
所以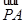 =2
=2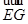 ,即PA//EG.
,即PA//EG.
而EGÌ平面EDB, 且PAË平面EDB,
因此PA//平面EDB.……………………4分
(2)证明:依题意得
B(1, 1, 0),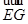 =(1,1, -1)
=(1,1, -1)
又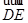 =(0,
=(0, 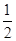 ,
, 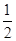 ),
),
故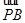 ×
×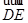 =0+
=0+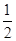 -
-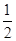 =0,所以PB^DE.
=0,所以PB^DE.
由已知EF^PB,且EF∩DE=E,所以PB^平面EFD.………………8分
(3)解:已知PB^EF,由(2)可知PB^DF,故ÐEFD是二面角C-PB-D的平面角,设点F的坐标为(x,y,z),则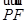 =(x, y, z–1).
=(x, y, z–1).
因为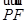 =k
=k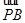 ,
,
所以(x, y, z-1)=k(1, 1, -1)=(k, k, -k),即x=k,y=k,z=1-k.
因为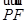 •
•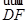 =0,
=0,
所以(1, 1, -1) • (k, k, 1-k)=k+k-1+k=3k-1=0.
所以k=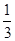 ,点F的坐标为(
,点F的坐标为(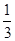 ,
,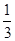 ,
,
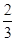 ).
).
又点E的坐标为(0, 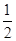 ,
, 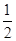 ).
).
所以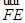 =(-
=(-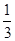 ,
,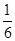 ,–
,–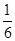 ).
).
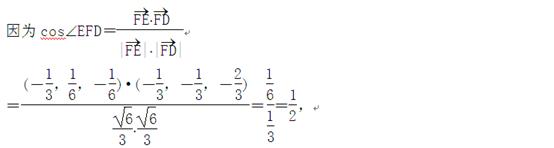
所以ÐEFD=60°,即二面角C-PB-D的大小为60°。………………13分
【解析】略

练习册系列答案
相关题目

 .
. 的最小正周期和最大值;
的最小正周期和最大值; 在区间
在区间 上的图象.
上的图象. ,且方程
,且方程 有两个不同的实数根,求实数m的取值范围.
有两个不同的实数根,求实数m的取值范围. 的函数
的函数 是奇函数.
是奇函数. 的值;(2)判断函数
的值;(2)判断函数 的单调性;
的单调性; ,不等式恒成立
,不等式恒成立 ,求k的取值范围.
,求k的取值范围. ,
,  ,
, .
. (∁
(∁ ; (2)若
; (2)若 ,求
,求 的取值范围.
的取值范围. 的所有棱长都为2,
的所有棱长都为2, 为
为 的中点。
的中点。 ∥平面
∥平面 ;
; 所成的角。www.7caiedu.cn
所成的角。www.7caiedu.cn

 为锐角,且
为锐角,且 ,函数
,函数 ,数列{
,数列{ }的首项
}的首项 .
. 的表达式;
的表达式; 中,若
中,若 A=2
A=2 ,BC=2,求
,BC=2,求 的前
的前 项和
项和