题目内容
10.求函数f(x)=4-2x2+x$\sqrt{1-{x}^{2}}$的最大值与最小值.分析 由1-x2≥0,可得-1≤x≤1,设x=sinα(-$\frac{π}{2}$≤α≤$\frac{π}{2}$),运用二倍角公式和两角和的正弦公式,及正弦函数的值域,即可得到所求最值.
解答 解:由1-x2≥0,可得-1≤x≤1,
设x=sinα(-$\frac{π}{2}$≤α≤$\frac{π}{2}$),
即有y=4-2sin2α+sinαcosα
=3+cos2α+$\frac{1}{2}$sin2α=3+$\frac{\sqrt{5}}{2}$sin(2α+θ)(θ为锐角,tanθ=2)
当2α+θ=$\frac{π}{2}$时,函数取得最大值3+$\frac{\sqrt{5}}{2}$;
当2α+θ=-$\frac{π}{2}$时,函数取得最大值3-$\frac{\sqrt{5}}{2}$.
点评 本题考查函数的最值的求法,注意运用三角换元和二倍角公式、两角和的正弦公式,以及正弦函数的值域,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.在△ABC中,内角A,B,C的对边分别是a,b,c,且有an+bn=cn(n≥3),则△ABC的形状为( )
| A. | 直角三角形 | B. | 锐角三角形 | ||
| C. | 钝角三角形 | D. | 直角或钝角三角形 |
20.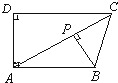 如图,已知四边形ABCD中AB∥CD,AD⊥AB,BP⊥AC,BP=PC,CD>AB,则经过某种翻折后以下线段可能会相互重合的是( )
如图,已知四边形ABCD中AB∥CD,AD⊥AB,BP⊥AC,BP=PC,CD>AB,则经过某种翻折后以下线段可能会相互重合的是( )
 如图,已知四边形ABCD中AB∥CD,AD⊥AB,BP⊥AC,BP=PC,CD>AB,则经过某种翻折后以下线段可能会相互重合的是( )
如图,已知四边形ABCD中AB∥CD,AD⊥AB,BP⊥AC,BP=PC,CD>AB,则经过某种翻折后以下线段可能会相互重合的是( )| A. | AB与AD | B. | AB与BC | C. | BD与BC | D. | AD与AP |