题目内容
如图在二面角α-
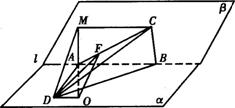
l-β中,A、B∈α,C、D∈l,ABCD为矩形,P∈β,PA⊥α,且PA=AD,MN依次是AB、PC的中点
(1)求二面角α-l-β的大小
(2)求证明:MN⊥AB
(3)求异面直线PA与MN所成角的大小
答案:
解析:
提示:
解析:
|
解: (1)连PD ∵PA⊥α,AD⊥l ∴PD⊥l ∴∠PDA为二面角α-l-β的平面角 在 RTΔPAD中∵ PA=PD∴∠PDA=45° ∴二面角α- l-β为45°(2)设E是DC的中点,连ME、NE ∵M、N、E分别为AB、PC、D的中点 ∴ ME∥AD,NE∥PD∴ME⊥l,NE⊥l ∴l⊥平面MEN ∵AB∥l ∴AB⊥平面MEN ∵MNÌ 平面MNE ∴MN^ AB (3)设Q是DP听中点,连NQ、AQ 则NQ∥DC,且NQ=1/2DC ∵AM∥DC,且AM=1/2AB=1/2DC ∴QN∥AM,QN=AM ∴QNMQ为平行四边形 ∴ AQ∥MN∴∠PAQ为PA与MN所成的角 ∵Δ PAQ为等腰直角三角形,AQ为斜边上的中线∴∠ PAQ=45°即 PA与MN所成角的大小为45° |
提示:
|
(1)用垂线法作二面角的平面角 (2)只要证明AB垂直于过MN的一个平面即可 (3)过点A作MN的平行线,转化为平面角求解 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在二面角M-l-N的一个M内有Rt△ABC,其中∠A=90°,顶点B、C在二面角的棱l上,AB、AC与平面N所成的角分别为α、β,若二面角M-l-N的大小为θ,则下面的关系式中正确的是( )
如图,在二面角M-l-N的一个M内有Rt△ABC,其中∠A=90°,顶点B、C在二面角的棱l上,AB、AC与平面N所成的角分别为α、β,若二面角M-l-N的大小为θ,则下面的关系式中正确的是( ) ⑴ 求二面角α- l-β的大小
⑴ 求二面角α- l-β的大小