题目内容
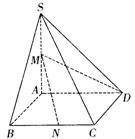
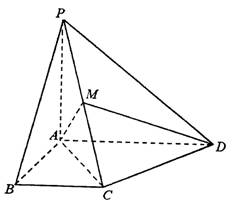
(理)如图,在四棱锥P—ABCD中,侧面PAD是正三角形且与底面ABCD垂直,底面ABCD是矩形,E是AB的中点,PC与平面ABCD所成的角为30°.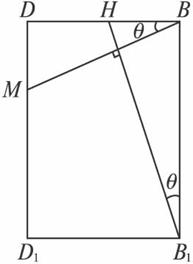
(1)若平面PAB∩平面PCD=l,试判断直线l与平面ABCD的关系,并加以证明;
(2)求平面PAB与平面PCD所成二面角的大小;
(3)当AD为多长时,点D到平面PCE的距离为2?
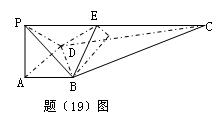
(文)在正四棱柱ABCD—A1B1C1D1中,BB1=2AB=4,E、F分别是棱AB与BC的中点.
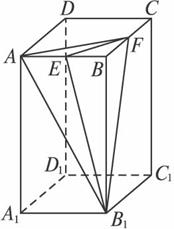
(1)求二面角EFB1B的平面角的正切值.
(2)在棱DD1上能否找到一点M,使BM⊥平面B1EF?若能,试确定M的位置;若不能,请说明理由.
解:(理)(1)l与面ABCD平行.证明:∵DC∥AB,DC![]() 面PAB,∴DC∥面PAB.∵DC
面PAB,∴DC∥面PAB.∵DC![]() 面PDC,面PAB∩面PCD=l,∴l∥DC.又l
面PDC,面PAB∩面PCD=l,∴l∥DC.又l![]() 面ABCD,DC
面ABCD,DC![]() 面ABCD,∴l∥面ABCD.
面ABCD,∴l∥面ABCD.
(2)由(1),可知面PAB∩面PCD=l.∵面PAD⊥面ABCD,ABCD为矩形,∴AB⊥面PAD.∵l∥DC∥AB,∴l⊥面PAD.∴l⊥AD.同理,l⊥AP.∴∠PAD为面PAB与面PDC所成二面角的平面角.∵△PAD是正三角形,∴面PAB与面PDC所成二面角大小为60°.
(3)设AD的中点为F,且AD=a,则PF⊥AD.∴∠PCF=30°.∴PF=![]() a.∴CF=
a.∴CF=![]() a,CD=
a,CD=![]() a.
a.
由VD—PEC=VP—DEC,得![]() S△DEC·PF=
S△DEC·PF=![]() S△PEC·2.∴
S△PEC·2.∴![]() ·a·
·a·![]() a·
a·![]() =2·S△PEC,①
=2·S△PEC,①
易求PE=EC=![]() a,PC=
a,PC=![]() a.∴S△PCE=
a.∴S△PCE=![]() |PC|
|PC|![]() .②
.②
由①②,得a=![]() .
.
(文)(1)过B点作BG⊥B1F,垂足为G点,连结EG.∵EB⊥面BB1C1C,根据三垂线定理,知∠EGB即为所求二面角的平面角.
EB=![]() AB=1,BG=
AB=1,BG=![]() .∴tan∠EGB=
.∴tan∠EGB=![]() ,二面角EFB1B的平面角的正切值为
,二面角EFB1B的平面角的正切值为![]() .
.
(2)设存在M点.

EF∩DB=H.已知BD=![]() ,BH=
,BH=![]() .∵EF⊥面BB1D1D,∴EF⊥B1H,EF⊥BM.在如图所示的截面中,BM⊥B1H,
.∵EF⊥面BB1D1D,∴EF⊥B1H,EF⊥BM.在如图所示的截面中,BM⊥B1H,
∴tanθ=![]() .∴DM=
.∴DM=![]() ,即存在点M,且D1M=
,即存在点M,且D1M=![]() 或DM=
或DM=![]() .
.

 阅读快车系列答案
阅读快车系列答案