题目内容
在平面中△ABC的角C的内角平分线CE分△ABC面积所成的比
=
,将这个结论类比到空间:在三棱锥A-BCD中,平面DEC平分二面角A-CD-B且与AB交于E,则类比的结论为______.

| S△ABC |
| S△BEC |
| AC |
| BC |

在平面中△ABC的角C的内角平分线CE分△ABC面积所成的比
=
,
将这个结论类比到空间:在三棱锥A-BCD中,平面DEC平分二面角A-CD-B且与AB交于E,
则类比的结论为根据面积类比体积,长度类比面积可得:
=
,
故答案为:
=
.
| S△ABC |
| S△BEC |
| AC |
| BC |
将这个结论类比到空间:在三棱锥A-BCD中,平面DEC平分二面角A-CD-B且与AB交于E,
则类比的结论为根据面积类比体积,长度类比面积可得:
| VA-CDE |
| VB-CDE |
| S△ACD |
| S△BDC |
故答案为:
| VA-CDE |
| VB-CDE |
| S△ACD |
| S△BDC |

练习册系列答案
相关题目
 与双曲线
与双曲线 的焦距相等.试将此命题推广到一般情形,使已知命题成为推广后命题的一个特例: .
的焦距相等.试将此命题推广到一般情形,使已知命题成为推广后命题的一个特例: .
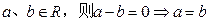 ”类比推出“
”类比推出“ ”
” ”类比推出
”类比推出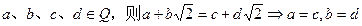 ”
”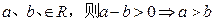 ”类比推出“若
”类比推出“若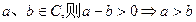 ”
”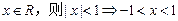 ”类比推出“若
”类比推出“若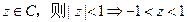 ”
”