题目内容
15. 如图:钝角三角形ABC的面积为18,最长边AB=12,BD平分∠ABC,点M、N分别是BD、BC上的动点,则CM+MN的最小值为3.
如图:钝角三角形ABC的面积为18,最长边AB=12,BD平分∠ABC,点M、N分别是BD、BC上的动点,则CM+MN的最小值为3.
分析 过点C作CE⊥AB于点E,交BD于点M,过点M作MN⊥BC于N,则CE=CM+ME=CM+MN的最小值,利用三角形ABC的面积为18,计算即可.
解答 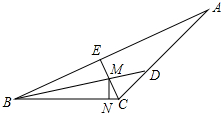 解:过点C作CE⊥AB于点E,交BD于点M,过点M作MN⊥BC于N,
解:过点C作CE⊥AB于点E,交BD于点M,过点M作MN⊥BC于N,
∵BD平分∠ABC,ME⊥AB于点E,MN⊥BC于N,
∴MN=ME,
∴CE=CM+ME=CM+MN的最小值.
∵三角形ABC的面积为18,AB=12,
∴$\frac{1}{2}$×12•CE=18,
∴CE=3.
即CM+MN的最小值为3.
故答案为:3.
点评 本题考查线段距离的最小值,找出最小值的情形是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
3.已知点A(0,1),曲线C:y=alnx恒过定点B,P为曲线C上的动点且$\overrightarrow{AP}$•$\overrightarrow{AB}$的最小值为2,则a=( )
| A. | -2 | B. | -1 | C. | 2 | D. | 1 |
10.已知全集U={1,2,3,4},A={1,4},B={2,4},则(∁UA)∩B=( )
| A. | ∅ | B. | {2} | C. | {4} | D. | {2,3,4} |
4.已知集合A={x|2<x<4},B={x|(x-1)(x-3)<0},则A∩B=( )
| A. | (1,3) | B. | (1,4) | C. | (2,3) | D. | (2,4) |