题目内容
已知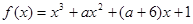 既有极大值又有极小值,则
既有极大值又有极小值,则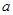 的取值范围为( )
的取值范围为( )
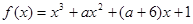 既有极大值又有极小值,则
既有极大值又有极小值,则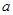 的取值范围为( )
的取值范围为( )A. | B. | C. | D. |
D
本试题主要是考查了一元二次函数极值的问题。
∵f(x)=x3+ax2+(a+6)x+1∴f'(x)=3x2+2ax+(a+6),∵函数f(x)=x3+ax2+(a+6)x+1既有极大值又有极小值,∴△=(2a)2-4×3×(a+6)>0,∴a>6或a<-3,故选D.
解决该试题的关键是一元三次函数有两个极值,则说明其导数为零的方程中,判别式大于零。
∵f(x)=x3+ax2+(a+6)x+1∴f'(x)=3x2+2ax+(a+6),∵函数f(x)=x3+ax2+(a+6)x+1既有极大值又有极小值,∴△=(2a)2-4×3×(a+6)>0,∴a>6或a<-3,故选D.
解决该试题的关键是一元三次函数有两个极值,则说明其导数为零的方程中,判别式大于零。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
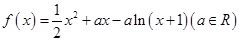 .
.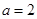 时,求函数
时,求函数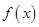 的极值;
的极值;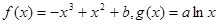 .
.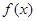 在
在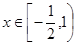 上的最大值为
上的最大值为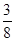 ,求实数
,求实数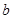 的值;
的值;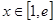 ,都有
,都有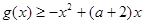 恒成立,求实数
恒成立,求实数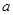 的取值范围;
的取值范围;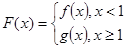 ,对任意给定的正实数
,对任意给定的正实数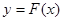 上是否存在两点
上是否存在两点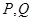 ,使得
,使得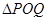 是以
是以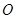 (
(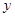 轴上?请说明理由.
轴上?请说明理由.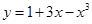 有( )
有( ) 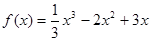 (
(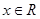 )的图象为曲线
)的图象为曲线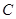 .
.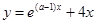 (
(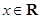 )有大于零的极值点,则实数
)有大于零的极值点,则实数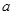 范围是 ( )
范围是 ( )



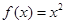 ,
, 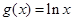 的图像分别交于点M,N,则当
的图像分别交于点M,N,则当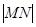 为最小时t的值为
为最小时t的值为


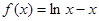 在区间
在区间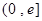 的最大值为( )
的最大值为( )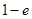
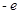
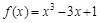 在闭区间[-3,0]上的最大值、最小值分别是 .
在闭区间[-3,0]上的最大值、最小值分别是 .