题目内容
函数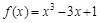 在闭区间[-3,0]上的最大值、最小值分别是 .
在闭区间[-3,0]上的最大值、最小值分别是 .
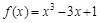 在闭区间[-3,0]上的最大值、最小值分别是 .
在闭区间[-3,0]上的最大值、最小值分别是 .3,-17
解:由f′(x)=3x2-3=0,得x=±1,
当x<-1时,f′(x)>0,
当-1<x<1时,f′(x)<0,
当x>1时,f′(x)>0,
故f(x)的极小值、极大值分别为f(-1)=3,f(1)=-1,
而f(-3)=-17,f(0)=1,
故函数f(x)=x3-3x+1在[-3,0]上的最大值、最小值分别是3、-17.
当x<-1时,f′(x)>0,
当-1<x<1时,f′(x)<0,
当x>1时,f′(x)>0,
故f(x)的极小值、极大值分别为f(-1)=3,f(1)=-1,
而f(-3)=-17,f(0)=1,
故函数f(x)=x3-3x+1在[-3,0]上的最大值、最小值分别是3、-17.

练习册系列答案
相关题目
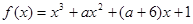 既有极大值又有极小值,则
既有极大值又有极小值,则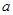 的取值范围为( )
的取值范围为( )



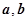 满足:
满足: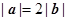 ,若函数
,若函数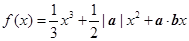 在
在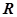 上有极值,设向量
上有极值,设向量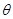 ,则
,则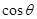 的取值范围为( )
的取值范围为( )
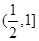


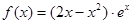 判断正确的是( )
判断正确的是( )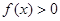 的解集是
的解集是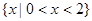 ;
;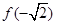 是极小值,
是极小值,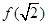 是极大值;
是极大值;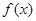 没有最小值,也没有最大值.
没有最小值,也没有最大值.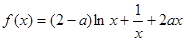 (a∈R).
(a∈R).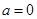 时,求
时,求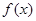 的极值;
的极值;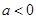 时,求
时,求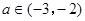 及
及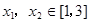 ,恒有
,恒有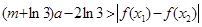
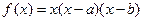 。
。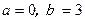 ,函数
,函数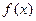 在
在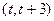 上既能取到极大值,又能取到极小值,求
上既能取到极大值,又能取到极小值,求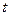 的取值范围;
的取值范围;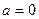 时,
时,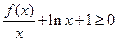 对任意的
对任意的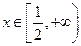 恒成立,求
恒成立,求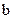 的取值范围;
的取值范围;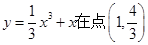 处的切线方程 。
处的切线方程 。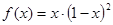 的极值点的个数是( )
的极值点的个数是( )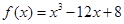 在区间
在区间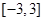 上的最大值与最小值分别为
上的最大值与最小值分别为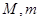 ,则
,则 .
.