Question

如图，在直三棱柱ABC-A₁B₁C₁中，AA₁=BC=AB=2，AB⊥BC．M、N分别是AC和BB₁的中点．
（1）求二面角B₁-A₁C-C₁的大小．
（2）证明：在AB上存在一个点Q，使得平面QMN⊥平面A₁B₁C，并求出BQ的长度．

Answer 1

分析：（1）建立空间直角坐标系，写出点的坐标与向量的坐标，再分别设出两个平面的法向量，然后利用法向量与平面上的向量数量积等于0，分别求出两个平面的一个法向量，再根据两个向量的有关运算求出两个向量的夹角，进而转化为二面角的平面角的余弦值求出答案即可．
（2）设Q（t，0，0），由两个平面垂直得到两个平面的法向量垂直，再分别求出两个平面的法向量利用其数量积等于0即可求出t的数值，进而得到答案．

解答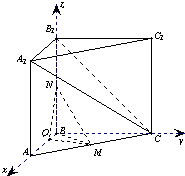：解：如图建立空间直角坐标系…（1分）
（1）由题意可得：A₁（2，0，2），B₁（0，0，2），C（0，2，0），C₁（0，2，2）
所以

A1C

=(-2，2，-2)，

A1B1

=(-2，0，0)，

CC1

=(0，0，2)
设平面A₁CB₁的法向量为

n

=(x1，y1，z1)，平面A₁CC₁的法向量为

m

=(x2，y2，z2)
则有

A1C • n =0 A1B1 • n =0

⇒

-2x1+2y1-2z1=0 -2x1=0

⇒

n

=(0，1，1)（3分）
同理：

A1C • m =0 CC1 • m =0

⇒

-2x2+2y2-2z2=0 -2z2=0

⇒

m

=(1，1，0)（5分）
设二面角B₁-A₁C-C₁为θ，由图形知此二面角是个锐角
所以cosθ=|cos＜

n

，

m

＞|=|

n • m

| n || m |

|=

1

2

∴二面角B₁-A₁C-C₁的大小为60°．…（7分）
（2）设Q（t，0，0）…（9分）
∵M（1，1，0），N（0，0，1）
∴

NQ

=(t，0，-1)，

NM

=(1，1，-1)，
设平面QMN的法向量为

u

=(x，y，z)
即有：

NQ • u =0 NM • u =0

⇒

tx-z=0 x+y-z=0

⇒

u

=(1，t-1，t)…（11分）
由（1）可知平面A₁CB₁的法向量为

n

=(0，1，1)
∵平面QMN⊥平面A₁B₁C
∴

u

•

n

=0，即2t-1=0，解得：t=

1

2

，
所以在AB上存在一个点Q，使得平面QMN⊥平面A₁B₁C，并且BQ=

1

2

．…（14分）

点评：解决此类问题的关键是熟练掌握利用空间向量求空间角的方法，求二面角的关键是正确求出平面的法向量，再利用向量之间的有关运算求出向量的夹角，进而把向量的夹角转化为空间角，本题要注意区分二面角与两个平面所成的角，本题求的是二面角．