题目内容
将直径为 的圆木锯成长方体横梁,横截面为矩形,横梁的强度同它的断面高的平方与宽
的圆木锯成长方体横梁,横截面为矩形,横梁的强度同它的断面高的平方与宽 的积成正比(强度系数为
的积成正比(强度系数为 ,
, ).要将直径为
).要将直径为 的圆木锯成强度最大的横梁,断面的宽
的圆木锯成强度最大的横梁,断面的宽 应是____________
应是____________ 
 的圆木锯成长方体横梁,横截面为矩形,横梁的强度同它的断面高的平方与宽
的圆木锯成长方体横梁,横截面为矩形,横梁的强度同它的断面高的平方与宽 的积成正比(强度系数为
的积成正比(强度系数为 ,
, ).要将直径为
).要将直径为 的圆木锯成强度最大的横梁,断面的宽
的圆木锯成强度最大的横梁,断面的宽 应是____________
应是____________ 
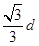
分析:据题意横梁的强度同它的断面高的平方与宽x的积成正比(强度系数为k,k>0)建立起强度函数,求出函数的定义域,再利用求导的方法求出函数取到最大值时的横断面的值。
解答:
设断面高为h,则h2=d2-x2,
横梁的强度函数f(x)=k?xh2,
所以f(x)=kx?(d2-x2),0<x<d。(5分)
当x∈(0,d)时,令f′(x)=k(d2-3x2)=0。
解得x=±
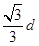 (舍负)。
(舍负)。当0<x<
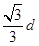 时,f′(x)>0;
时,f′(x)>0;当
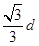 <x<d时,f′(x)<0。
<x<d时,f′(x)<0。因此,函数f(x)在定义域(0,d)内只有一个极大值点x=
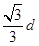 。
。所以f(x)在x=
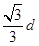 处取最大值,就是横梁强度的最大值。
处取最大值,就是横梁强度的最大值。即当断面的宽为
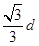 时,横梁的强度最大。
时,横梁的强度最大。点评:考查据实际意义建立相关的函数,再根据函数的特征选择求导的方法来求最值。

练习册系列答案
相关题目
 的图象大致是
的图象大致是

 ,猜想
,猜想 的表达式为
的表达式为 ;
; ;
; ;
; .
.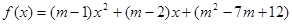 为偶函数,则
为偶函数,则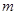 的值
的值

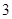

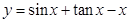 ;②
;②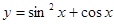 ;③
;③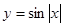 ;④
;④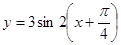 ,属于偶函数的有( )
,属于偶函数的有( ) 满足
满足 时,
时, ,若
,若 ,则
,则 = 。
= 。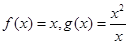



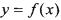 在及上有定义对雅定的正数M,定义函数
在及上有定义对雅定的正数M,定义函数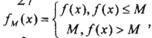 则称函数
则称函数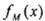 为
为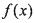 的“孪生函数”.若给定函数
的“孪生函数”.若给定函数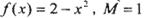 ,则
,则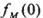 的值为( )
的值为( )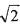
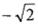
 的定义域为R,求实数m的取值范围
的定义域为R,求实数m的取值范围