题目内容
观察下列等式
1=1
2+3+4=9
3+4+5+6+7=25
4+5+6+7+8+9+10=49
…
照此规律,第n个等式为 _________ .
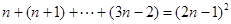
解析试题分析:根据题意,
第一个式子的左边是1,只有1个数,其中1=2×1-1,
第二个式子的左边是从2开始的3个数的和,其中3=2×2-1;
第三个式子的左边是从3开始的5个数的和,其中5=2×3-1;
第四个式子的左边是从4开始的7个数的和,其中7=2×4-1;
以此类推,第n个式子的左边是从n开始的(2n-1)个数的和,右边是求和的结果;
所以第n个等式为: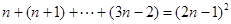 .
.
考点:归纳推理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
观察下列事实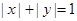 的不同整数解
的不同整数解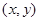 的个数为4,
的个数为4,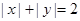 的不同整数解
的不同整数解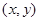 的个数为8,
的个数为8,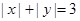 的不同整数解
的不同整数解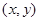 的个数为12,……,则
的个数为12,……,则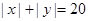 的不同整数解
的不同整数解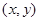 的个数为( )
的个数为( )
| A.76 | B.80 | C.86 | D.92 |
有一段演绎推理是这样的“有些有理数是真分数,整数是有理数,则整数是真分数”该结论显然是错误的,其原因是
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.非以上错误 |
用数学归纳法证明不等式“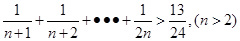 ”的过程中,由n=k到n=k+1时,不等式的左边( )
”的过程中,由n=k到n=k+1时,不等式的左边( )
A.增加了一项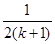 |
B.增加了两项 |
C.增加了一项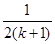 ,又减少了一项 ,又减少了一项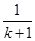 |
D.增加了两项 ,又减少了一项 ,又减少了一项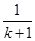 |
用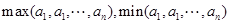 分别表示
分别表示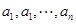 中的最大与最小者,有下列结论:
中的最大与最小者,有下列结论:
①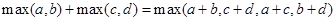 ;
;
②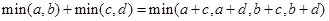 ;
;
③若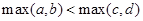 ,则
,则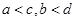 ;
;
④若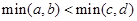 ,则
,则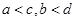 。
。
其中正确结论的个数是( )
| A.0 | B.1 | C.2 | D.3 |
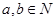 ,
,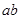 可被
可被 整除,那么
整除,那么 中至少有一个能被
中至少有一个能被 、
、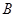 、
、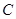 三个城市时,
三个城市时,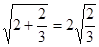 ,
,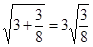 ,
,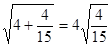 , .,类比这些等式,若
, .,类比这些等式,若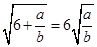 (
(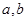 均为正实数),则
均为正实数),则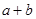 = .
= .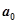 ,用
,用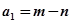 ,然后继续对
,然后继续对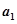 重复上述变换,得数
重复上述变换,得数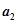 ,…,如此进行下去,卡普耶卡发现,无论
,…,如此进行下去,卡普耶卡发现,无论