题目内容
(本小题14分)
已知直线L被两平行直线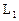 :
: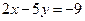 与
与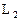 :
: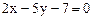 所截线段AB的中点恰在直线
所截线段AB的中点恰在直线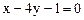 上,已知
上,已知 圆
圆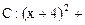
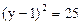 .
.
(Ⅰ)求两平行直线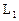 与
与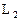 的距离;
的距离;
(Ⅱ)证明直线L与圆C恒有两个交 点;
点;
 (Ⅲ)求直线L被圆C截得的弦长最小时的方程
(Ⅲ)求直线L被圆C截得的弦长最小时的方程 .
.
已知直线L被两平行直线
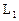 :
: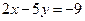 与
与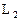 :
: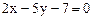 所截线段AB的中点恰在直线
所截线段AB的中点恰在直线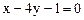 上,已知
上,已知 圆
圆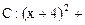
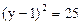 .
. (Ⅰ)求两平行直线
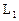 与
与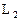 的距离;
的距离;(Ⅱ)证明直线L与圆C恒有两个交
 点;
点; (Ⅲ)求直线L被圆C截得的弦长最小时的方程
(Ⅲ)求直线L被圆C截得的弦长最小时的方程 .
.(1)
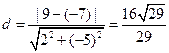
(2)略
(3
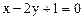
(Ⅰ)解:两平行直线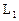 与
与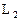 的距离
的距离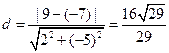 ………3分
………3分
(Ⅱ)证明(法一):设线段AB的中点P的坐标(a,b),由P到L1,、L2的距离相等,得
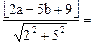
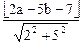 ,
,
经整理得,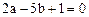 ,又点P在直线x-4y-1=0上,所以
,又点P在直线x-4y-1=0上,所以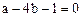
解方程组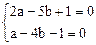 得
得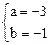 即点P的坐标(-3,-1),………7分
即点P的坐标(-3,-1),………7分
所以直线L恒过点P(-3,-1);…………… 8分
将点P(-3,-1)代入圆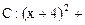
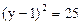 ,可得
,可得 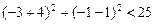
所以点P(-3,-1)在圆内,从而过点P的直线L与圆C恒有两个交点.………10分
(Ⅲ)解:当PC与直线L垂直时,弦长最小,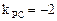 ,所以直线L的斜率为
,所以直线L的斜率为
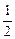 ,所以直线L的方程为:
,所以直线L的方程为: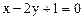 .……………………………14分
.……………………………14分
(Ⅱ)法二:设线段AB的中点P必经过直线: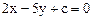 ,由已知,得
,由已知,得
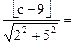
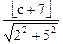 ,
,
所以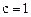 ,所以
,所以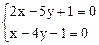 ,得点P(-3,-1),以下同法一
,得点P(-3,-1),以下同法一
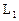 与
与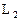 的距离
的距离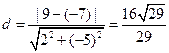 ………3分
………3分(Ⅱ)证明(法一):设线段AB的中点P的坐标(a,b),由P到L1,、L2的距离相等,得
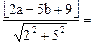
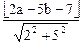 ,
,经整理得,
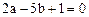 ,又点P在直线x-4y-1=0上,所以
,又点P在直线x-4y-1=0上,所以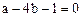
解方程组
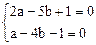 得
得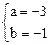 即点P的坐标(-3,-1),………7分
即点P的坐标(-3,-1),………7分所以直线L恒过点P(-3,-1);…………… 8分
将点P(-3,-1)代入圆
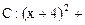
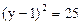 ,可得
,可得 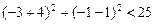
所以点P(-3,-1)在圆内,从而过点P的直线L与圆C恒有两个交点.………10分
(Ⅲ)解:当PC与直线L垂直时,弦长最小,
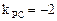 ,所以直线L的斜率为
,所以直线L的斜率为
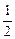 ,所以直线L的方程为:
,所以直线L的方程为: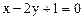 .……………………………14分
.……………………………14分(Ⅱ)法二:设线段AB的中点P必经过直线:
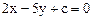 ,由已知,得
,由已知,得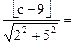
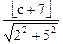 ,
,所以
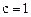 ,所以
,所以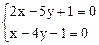 ,得点P(-3,-1),以下同法一
,得点P(-3,-1),以下同法一
练习册系列答案
相关题目
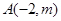 和
和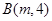 的直线与直线
的直线与直线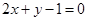 平行,则
平行,则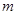 的值为( )
的值为( )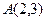 ,直线
,直线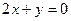 平分圆C,且圆C与直线
平分圆C,且圆C与直线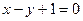 相交的弦长为
相交的弦长为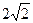 ,
, 的倾斜角是( )
的倾斜角是( ) 22
22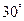



 在
在 轴上的截距是
轴上的截距是 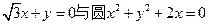 相交于A、B两点,则|AB|等于
相交于A、B两点,则|AB|等于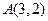 且垂直于直线
且垂直于直线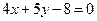 的直线方程为
的直线方程为 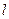 沿x轴正方向平移2个单位,再沿y轴负方向平移1个单位,又回到原来的位置,则直线
沿x轴正方向平移2个单位,再沿y轴负方向平移1个单位,又回到原来的位置,则直线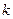 =_______
=_______