题目内容
(本小题满分12分)已知点P(6,4)与定直线l1:y=4x,直线l2过点P与直线l1相交于第一象限内的点Q,且与x轴的正半轴交于点M,求使△OMQ面积最小的直线l2的方程.
l2的直线方程为x+y-10=0.
:设M(m,0),则直线l2的方程为
4x+(m-6)y-4m="0. " (*)
与y=4x联立方程组,得yQ=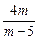 .
.
∵yQ>0,且m>0,
∴S△OMQ=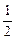 ·m·yQ=
·m·yQ=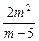 ,且m-5>0.
,且m-5>0.
令m-5=t,则t>0,
∴S△OMQ=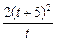 =2(10+t+
=2(10+t+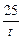 )
)
≥2(10+2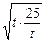 )=40.
)=40.
当且仅当t=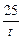 ,即t=5时,S△OMQ取最小值40.
,即t=5时,S△OMQ取最小值40.
此时,m=10.把m=10代入(*)式,得
l2的直线方程为x+y-10=0.
4x+(m-6)y-4m="0. " (*)
与y=4x联立方程组,得yQ=
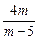 .
.∵yQ>0,且m>0,
∴S△OMQ=
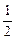 ·m·yQ=
·m·yQ=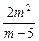 ,且m-5>0.
,且m-5>0.令m-5=t,则t>0,
∴S△OMQ=
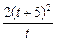 =2(10+t+
=2(10+t+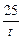 )
)≥2(10+2
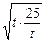 )=40.
)=40.当且仅当t=
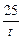 ,即t=5时,S△OMQ取最小值40.
,即t=5时,S△OMQ取最小值40.此时,m=10.把m=10代入(*)式,得
l2的直线方程为x+y-10=0.

练习册系列答案
相关题目
 ;②
;② ;③
;③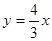 ;④
;④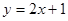 .其中为“B型直线”的是 ( )
.其中为“B型直线”的是 ( )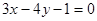 的距离为2的直线方程为 ( )
的距离为2的直线方程为 ( )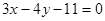 B.
B.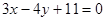
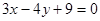 D
D 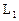 :
: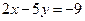 与
与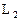 :
: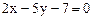 所截线段AB的中点恰在直线
所截线段AB的中点恰在直线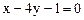 上,已知
上,已知 圆
圆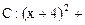
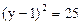 .
.  点;
点; (Ⅲ)求直线L被圆C截得的弦长最小时的方程
(Ⅲ)求直线L被圆C截得的弦长最小时的方程 .
. 并且与极轴垂直的直线方程是
并且与极轴垂直的直线方程是
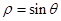


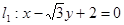 与
与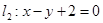 的夹角的大小是____
的夹角的大小是____ 与直线
与直线 互相垂直,则
互相垂直,则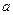 的值是 ( )
的值是 ( ) 及圆
及圆 ,则过点
,则过点 ,且在圆上截得的弦为最长的弦所在的直线方程是
,且在圆上截得的弦为最长的弦所在的直线方程是


