题目内容
设各项均为正数的数列{an}和{bn}满足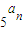 ,
,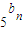 ,
,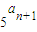 成等比数列,lgbn,lgan+1,lgbn+1成等差数列,且a1=1,b1=2,a2=3,求通项an、bn.
成等比数列,lgbn,lgan+1,lgbn+1成等差数列,且a1=1,b1=2,a2=3,求通项an、bn.
【答案】分析:由等比中项、等差中项的性质得an+1=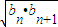 递推出an=
递推出an=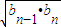 (n≥2).
(n≥2).
解答:解:∵5an,5bn,5an+1成等比数列,
∴(5an)2=5bn•5an+1,即2bn=an+an+1.①
又∵lgbn,lgan+1,lgbn+1成等差数列,
∴2lgan+1=lgbn+lgbn+1,即an+12=bn•bn+1.②
由②及ai>0,bj>0(i、j∈N*)可得
an+1=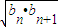 .③
.③
∴an=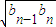 (n≥2).④
(n≥2).④
将③④代入①可得2bn=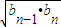 +
+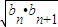 (n≥2),
(n≥2),
∴2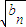 =
=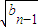 +
+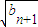 (n≥2).
(n≥2).
∴数列{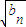 }为等差数列.
}为等差数列.
∵b1=2,a2=3,a22=b1•b2,∴b2= .
.
∴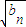 =
=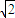 +(n-1)(
+(n-1)(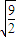 -
-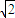 )
)
=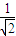 (n+1)(n=1也成立).
(n+1)(n=1也成立).
∴bn=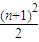 .
.
∴an=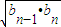 =
=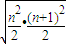
=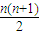 (n≥2).
(n≥2).
又当n=1时,a1=1也成立.
∴an=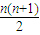 .
.
点评:本题主要考查了直线与圆锥曲线的综合问题呢.解题过程中注意由Sn求an时要注意验证a1与S1是否一致.
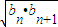 递推出an=
递推出an=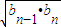 (n≥2).
(n≥2).解答:解:∵5an,5bn,5an+1成等比数列,
∴(5an)2=5bn•5an+1,即2bn=an+an+1.①
又∵lgbn,lgan+1,lgbn+1成等差数列,
∴2lgan+1=lgbn+lgbn+1,即an+12=bn•bn+1.②
由②及ai>0,bj>0(i、j∈N*)可得
an+1=
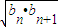 .③
.③∴an=
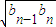 (n≥2).④
(n≥2).④将③④代入①可得2bn=
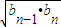 +
+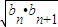 (n≥2),
(n≥2),∴2
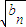 =
=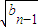 +
+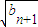 (n≥2).
(n≥2).∴数列{
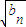 }为等差数列.
}为等差数列.∵b1=2,a2=3,a22=b1•b2,∴b2=
 .
.∴
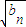 =
=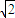 +(n-1)(
+(n-1)(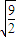 -
-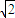 )
)=
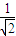 (n+1)(n=1也成立).
(n+1)(n=1也成立).∴bn=
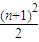 .
.∴an=
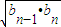 =
=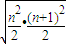
=
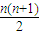 (n≥2).
(n≥2).又当n=1时,a1=1也成立.
∴an=
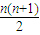 .
.点评:本题主要考查了直线与圆锥曲线的综合问题呢.解题过程中注意由Sn求an时要注意验证a1与S1是否一致.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目