题目内容
对于数列 ,如果存在一个正整数
,如果存在一个正整数 ,使得对任意的
,使得对任意的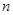
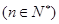 都有
都有 成立,那么就把这样一类数列
成立,那么就把这样一类数列 称作周期为
称作周期为 的周期数列,
的周期数列, 的最小正值称作数列
的最小正值称作数列 的最小正周期,以下简称周期。例如当
的最小正周期,以下简称周期。例如当 时,
时, 是周期为
是周期为 的周期数列;当
的周期数列;当 时,
时, 是周期为
是周期为 的周期数列。设数列
的周期数列。设数列 满足
满足
 .
.
(1)若数列 是周期为
是周期为 的周期数列,则常数
的周期数列,则常数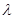 的值是
;
的值是
;
(2)设数列 的前
的前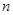 项和为
项和为 ,若
,若 ,则
,则 .
.
【答案】
(1)-1, (2) 3
【解析】解:由(1)数列{an}是周期为3的数列,
得an+3=an,且 an+2=λ an+1-an
an+3=λan+2-an+1 ⇒(λ+1)(an+2-an+1)=0,即λ=-1.
(2)利用数列的递推关系
an+3= an+2-an+1,进行分析,数列的特点,得到前2012项的为为3.

练习册系列答案
相关题目
对于数列{an},如果存在正实数M,使得数列中每一项的绝对值均不大于M,那么称该数列为有界的,否则称它为无界的.在以下各数列中,无界的数列为( )
| A、a1=2,an+1=-2an+3 | ||
B、a1=2,an+1=
| ||
| C、a1=2,an+1=arctanan+1 | ||
D、a1=2,an+1=2
|