题目内容
设函数 .
.(I)求
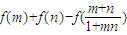 的值;
的值;(II)若关于x的方程
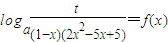 在x∈[0,1)上有实数解,求实数t的取值范围.
在x∈[0,1)上有实数解,求实数t的取值范围.(III)若f(x)的反函数f-1(x)的图象过点
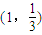 ,求证:
,求证: .
.
【答案】分析:(I)直接把变量代入,整理即可得到结论;
(II)先把所求问题转化为t=(1+x)(2x2-5x+5),在x∈[0,1)上有实数解,通过求其导数,即可求出其最大最小值,进而得到结论.
(III)先根据条件求出a,再结合放缩法即可得到结论的证明.
解答:解:(I)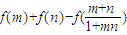
=loga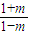 +loga
+loga -f(
-f(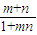 )
)
=loga( •
•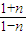 )-f(
)-f(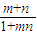 )
)
=loga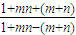 -f(
-f(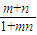 )
)
=loga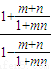 -f(
-f(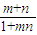 )
)
=f( )-f(
)-f(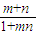 )
)
=0.
(II)因为关于x的方程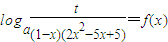 在x∈[0,1)上有实数解,
在x∈[0,1)上有实数解,
所以:loga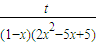 =loga
=loga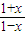 ;
;
所以: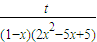 =
=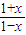 在x∈[0,1)上有实数解;
在x∈[0,1)上有实数解;
所以:t=(1+x)(2x2-5x+5),在x∈[0,1)上有实数解,
因为:t′=6x(x-1),且x∈[0,1)时,t′(x)<0,
所以:t(x)在[0,1)上单调递减,
所以:t(1)<t(x)≤t(0),即4<t≤5,
所以:实数t的取值范围是:t(4,5].
(III)因为f-1(x)的图象过点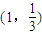 ,
,
所以: =
=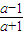 ,解得a=2.
,解得a=2.
所以:f-1(x)=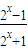 =1-
=1- ;
;
得:1-f-1(x)=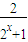 ;
;
当n≥3时,
所以:(1-f-1(1))+(1-f-1(2))+(1-f-1(3))+…+(1-f-1(n))
=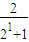 +
+ +
+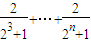
<2( +
+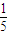 +
+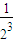 +…+
+…+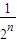 )
)
=2( +
+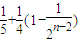 )
)
<2( +
+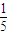 +
+ )=
)=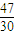 .
.
所以: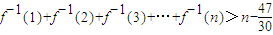 .
.
因为:当n=1或n=2时,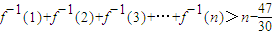 成立.
成立.
故 对所有的正整数n成立.
对所有的正整数n成立.
点评:本题主要考查导函数的正负与原函数的单调性之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.其中涉及到不等式的证明.
(II)先把所求问题转化为t=(1+x)(2x2-5x+5),在x∈[0,1)上有实数解,通过求其导数,即可求出其最大最小值,进而得到结论.
(III)先根据条件求出a,再结合放缩法即可得到结论的证明.
解答:解:(I)
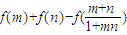
=loga
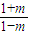 +loga
+loga -f(
-f(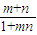 )
)=loga(
 •
•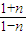 )-f(
)-f(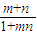 )
)=loga
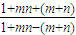 -f(
-f(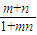 )
)=loga
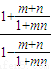 -f(
-f(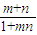 )
)=f(
 )-f(
)-f(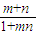 )
)=0.
(II)因为关于x的方程
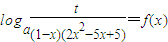 在x∈[0,1)上有实数解,
在x∈[0,1)上有实数解,所以:loga
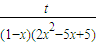 =loga
=loga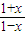 ;
;所以:
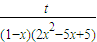 =
=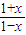 在x∈[0,1)上有实数解;
在x∈[0,1)上有实数解;所以:t=(1+x)(2x2-5x+5),在x∈[0,1)上有实数解,
因为:t′=6x(x-1),且x∈[0,1)时,t′(x)<0,
所以:t(x)在[0,1)上单调递减,
所以:t(1)<t(x)≤t(0),即4<t≤5,
所以:实数t的取值范围是:t(4,5].
(III)因为f-1(x)的图象过点
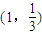 ,
,所以:
 =
=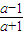 ,解得a=2.
,解得a=2.所以:f-1(x)=
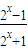 =1-
=1- ;
;得:1-f-1(x)=
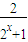 ;
;当n≥3时,
所以:(1-f-1(1))+(1-f-1(2))+(1-f-1(3))+…+(1-f-1(n))
=
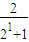 +
+ +
+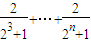
<2(
 +
+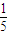 +
+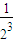 +…+
+…+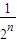 )
)=2(
 +
+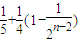 )
)<2(
 +
+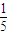 +
+ )=
)=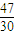 .
.所以:
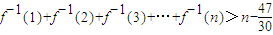 .
.因为:当n=1或n=2时,
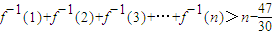 成立.
成立.故
 对所有的正整数n成立.
对所有的正整数n成立.点评:本题主要考查导函数的正负与原函数的单调性之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.其中涉及到不等式的证明.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
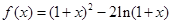 .
.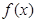 的单调区间;
的单调区间;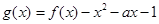 在区间
在区间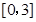 上的最小值.
上的最小值. ,
, 的最小正周期以及单调增区间;
的最小正周期以及单调增区间; 时,求
时,求 ,求
,求 的值.
的值.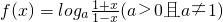 .
.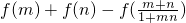 的值;
的值;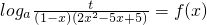 在x∈[0,1)上有实数解,求实数t的取值范围.
在x∈[0,1)上有实数解,求实数t的取值范围.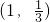 ,求证:
,求证: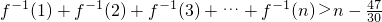 .
.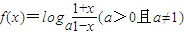 .
. 的值;
的值;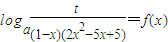 在x∈[0,1)上有实数解,求实数t的取值范围.
在x∈[0,1)上有实数解,求实数t的取值范围.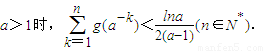 .
.