题目内容
(本小题满分12分)设函数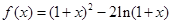 .
.
(I)求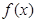 的单调区间;
的单调区间;
(II)当0<a<2时,求函数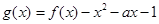 在区间
在区间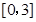 上的最小值.
上的最小值.
【答案】
(1)函数的单调递增区间为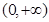 ,单调递减区间为
,单调递减区间为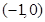 .
.
(2)当 时,
时,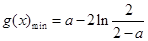 ;当
;当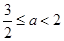 时,
时, .
.
【解析】导数主要考查有导数有关的概念、计算和应用(定积分的应用)。利用导数工具研究函数的有关性质,把导数应用于单调性、极值等传统、常规问题的同时,进一步升华到处理与不等式的证明、解析几何、方程的解及函数零点等问题。
解:(I)定义域为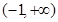 . ………………………1分
. ………………………1分
 .
.
令 ,则
,则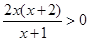 ,所以
,所以 或
或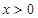 . ……………………3分
. ……………………3分
因为定义域为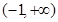 ,所以
,所以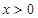 .
.
令 ,则
,则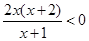 ,所以
,所以 .
.
因为定义域为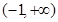 ,所以
,所以 . ………………………5分
. ………………………5分
所以函数的单调递增区间为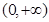 ,
,
单调递减区间为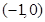 .
………………………7分
.
………………………7分
(II)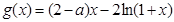 (
( ).
).
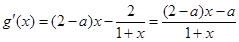 .
.
因为0<a<2,所以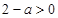 ,
,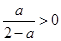 .令
.令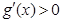 可得
可得 .……9分
.……9分
所以函数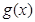 在
在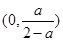 上为减函数,在
上为减函数,在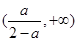 上为增函数.
上为增函数.
①当 ,即
,即 时,
时,
在区间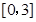 上,
上,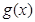 在
在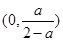 上为减函数,在
上为减函数,在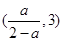 上为增函数.
上为增函数.
所以 . ………………………10分
. ………………………10分
②当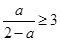 ,即
,即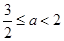 时,
时,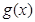 在区间
在区间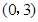 上为减函数.
上为减函数.
所以 .
.
综上所述,当 时,
时,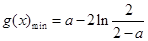 ;
;
当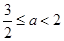 时,
时, .
………………12分
.
………………12分

练习册系列答案
相关题目