Question

（本题满分15分）

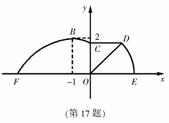
如图，某市准备在道路EF的一侧修建一条运动比赛道，赛道的前一部分为曲线段FBC，该曲线段是函数 ，时的图象，且图象的最高点为B（－1，2）。赛道的中间部分为长千米的直线跑道CD，且CD// EF。赛道的后一部分是以O为圆心的一段圆弧．

（1）求的值和的大小；

（2）若要在圆弧赛道所对应的扇形ODE区域内建一个“矩形草坪”，矩形的一边在道路EF上，一个顶点在半径OD上，另外一个顶点P在圆弧上，且，求当“矩形草坪”的面积取最大值时的值．

Answer 1

（本题满分15分）

解：（1）由条件，得，． ……………………………………………………………2分

           ∵，∴．……………………………………………………………………4分

           ∴ 曲线段FBC的解析式为．

           当x=0时，．又CD=，∴．……………7分

        （2）由（1），可知．

又易知当“矩形草坪”的面积最大时，点P在弧DE上，故．……………8分

设，，“矩形草坪”的面积为

     

      =．…………………………………13分

∵，故取得最大值．………………………15分