题目内容
【题目】已知抛物线C:y2=4x,焦点为F,过点P(﹣1,0)作斜率为k(k>0)的直线l与抛物线C交于A,B两点,直线AF,BF分别交抛物线C于M,N两点,若 ![]() +
+ ![]() =18,则k= .
=18,则k= .
【答案】![]()
【解析】解:由题意,图形关于x轴对称,A,B,P三点共线,可得 ![]() =
= ![]() .
.
由焦半径公式|AF|=x1+1=|NF|,||BF|=x2+1=|MF|,
∴ ![]() +
+ ![]() =
= ![]() +
+ ![]() =18,∴(y1+y2)2=20y1y2 ,
=18,∴(y1+y2)2=20y1y2 ,
由 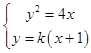 ,可得ky2﹣4y+4k=0,
,可得ky2﹣4y+4k=0,
∴y1+y2= ![]() ,y1y2=4,∴
,y1y2=4,∴ ![]() =80,
=80,
∵k>0,∴k= ![]() .
.
所以答案是 ![]() .
.
【考点精析】通过灵活运用抛物线的定义,掌握平面内与一个定点![]() 和一条定直线
和一条定直线![]() 的距离相等的点的轨迹称为抛物线.定点
的距离相等的点的轨迹称为抛物线.定点![]() 称为抛物线的焦点,定直线
称为抛物线的焦点,定直线![]() 称为抛物线的准线即可以解答此题.
称为抛物线的准线即可以解答此题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目