题目内容
9.如果四棱锥的四条侧棱都相等,就称它为“等腰四棱锥”,四条侧棱称为它的腰.以下4个命题中,假命题是A.等腰四棱锥的腰与底面所成的角都相等
B.等腰四棱锥的侧面与底面所成的二面角都相等或互补
C.等腰四棱锥的底面四边形必存在外接圆
D.等腰四棱锥的各顶点必在同一球面上
B
解析:如图作PH⊥面AC,则由射影定理可知HA=HB=HC=HD,从面底面顶点ABCD在的以H为圆心的圆上,且四条腰与底面所成的角均为arcsin的![]() ,从而排除A、C.
,从而排除A、C.
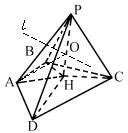
又PH上任一点到底面顶点距离都相等。△PHA中,作PA中线l交PH于O。则PO=OA=OB=OC=OD,从而四棱锥各顶点在以O为球心的球上,从而排除D。
B项可举出如下反例
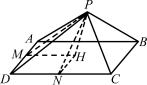
底面ABCD为矩形,如AB≠CD,则∠PMH≠∠PNH。

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目