题目内容
（本小题满分10分）选修4—4：坐标系与参数方程：
已知圆C的参数方程为 （φ为参数）；
（1）把圆C的参数方程化成直角坐标系中的普通方程；
（2）以直角坐标系的原点O为极点，x轴的正半轴为极轴建立极坐标系，把（1）中的圆C的普通方程化成极坐标方程；设圆C和极轴正半轴的交点为A，写出过点A且垂直于极轴的直线的极坐标方程。
已知圆C的参数方程为 （φ为参数）；
（1）把圆C的参数方程化成直角坐标系中的普通方程；
（2）以直角坐标系的原点O为极点，x轴的正半轴为极轴建立极坐标系，把（1）中的圆C的普通方程化成极坐标方程；设圆C和极轴正半轴的交点为A，写出过点A且垂直于极轴的直线的极坐标方程。
（1）由sin2φ+cos2φ=1及2 cosφ=x-2，2sinφ=y得圆C的普通方程为（x-2）2+y2="4" 。（4分）
（2）由得：（ρcosθ-2）2+ρ2sin2θ=4，得圆C的极坐标方程为ρ=4cosθ；
因为圆C与极轴正半轴交点为（4，0），所以所求直线的极坐标方程为ρcosθ="4" 。（10分）
（2）由得：（ρcosθ-2）2+ρ2sin2θ=4，得圆C的极坐标方程为ρ=4cosθ；
因为圆C与极轴正半轴交点为（4，0），所以所求直线的极坐标方程为ρcosθ="4" 。（10分）
略
练习册系列答案
期末集结号系列答案
相关题目
中，求过椭圆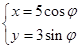
（
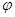为参数）的右焦点且与直线
（
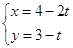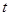为参数）平行的直线的普通方程。
，
，
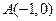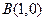动点P满足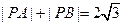
，记动点P的轨迹为W．
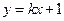与曲线W交于不同的两点C，D，若存在点
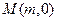，使得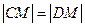
成立，求实数m的取值范围．
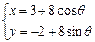上，则x0、y0的取值范围是（ ）
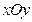中，以O为极点，
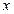轴正半轴为极轴建立极坐标系，直线
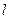的极坐标方程为
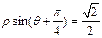．圆O的参数方程为
，（
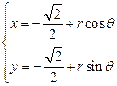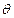为参数，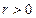
）
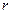为何值时，圆O上的点到直线
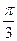，则直线l的参数方程可为( )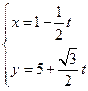
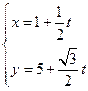
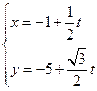
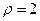上的点到直线
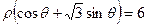的距离的最小值是 .
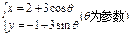，直线l的参数方程为
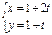（t为参数），则直线l被曲线C截得的弦长为 。
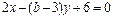与直线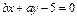
互相垂直，则
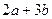的最小值为 。
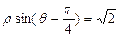和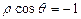
的直角坐标方程是什么？并求它们交点的极坐标？