题目内容
已知点C(4,0)和直线l:x=1,过动点P作PQ⊥l,垂足为Q,且(| PC |
| PQ |
| PC |
| PQ |
(1)求点P的轨迹方程,
(2)过点C的直线m与点P的轨迹交于两点M(x1,y1),N(x2,y2),其中x1x2>0,点B(1,0),若△BMN的面积为36
| 5 |
分析:(1)由|
|2-4|
|2=0,知|
|=2|
|,设P(x,y),代入得
=2|x-1|,整理得点P的轨迹方程.
(2)由题知直线m的斜率不为0,且点C(4,0)为双曲线
-
=1 的右焦点,设m的方程为x=ty+4,由
得(3t2-1)y2+24ty+36=0,所以x1x2=(ty1+4)(ty2+4)=t2y1y2+4t(y1+y2)+16.由此入手能够求出直线m的方程.
| PC |
| PQ |
| PC |
| PQ |
| (x-4)2+y2 |
(2)由题知直线m的斜率不为0,且点C(4,0)为双曲线
| x2 |
| 4 |
| y2 |
| 12 |
|
解答:解:(1)由题|
|2-4|
|2=0,∴|
|=2|
|,
设P(x,y),
代入得
=2|x-1|,
整理得点P的轨迹方程为:
-
=1,(3分)
(2)由题知直线m的斜率不为0,
且点C(4,0)为双曲线
-
=1的右焦点,
设m的方程为x=ty+4,由
得(3t2-1)y2+24ty+36=0,(5分)
易知3t2-1≠0且
,
∴x1x2=(ty1+4)(ty2+4)=t2y1y2+4t(y1+y2)+16,(7分)
由x1x2>0得
<0?t2<
,S△BMN=
|BC||y1-y2|=
×
=
=
=36
,(10分)
解得t2=
或t2=
(舍),
∴t2=
?t=±
,
直线m的方程为:2x+y-8=0或2x-y-8=0.(12分)
| PC |
| PQ |
| PC |
| PQ |
设P(x,y),
代入得
| (x-4)2+y2 |
整理得点P的轨迹方程为:
| x2 |
| 4 |
| y2 |
| 12 |
(2)由题知直线m的斜率不为0,
且点C(4,0)为双曲线
| x2 |
| 4 |
| y2 |
| 12 |
设m的方程为x=ty+4,由
|
易知3t2-1≠0且
|
∴x1x2=(ty1+4)(ty2+4)=t2y1y2+4t(y1+y2)+16,(7分)
由x1x2>0得
| 3t2+4 |
| 3t2-1 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
| ||
| |3t2-1| |
18
| ||
| |3t2-1| |
18
| ||
| 1-3t2 |
| 5 |
解得t2=
| 1 |
| 4 |
| 19 |
| 45 |
∴t2=
| 1 |
| 4 |
| 1 |
| 2 |
直线m的方程为:2x+y-8=0或2x-y-8=0.(12分)
点评:本题考查轨迹方程的求法和直线方程的求法,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 P是动点,作
P是动点,作 垂足为Q,且
垂足为Q,且 设P点的轨迹是曲线M。
设P点的轨迹是曲线M。 若存在,求出直线m的方程;若不存在,说明理由。
若存在,求出直线m的方程;若不存在,说明理由。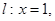 P是动点,作
P是动点,作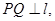 垂足为Q,且
垂足为Q,且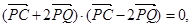 设P点的轨迹是曲线M。
设P点的轨迹是曲线M。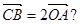 若存在,求出直线m的方程;若不存在,说明理由。
若存在,求出直线m的方程;若不存在,说明理由。