题目内容
已知点C(4,0)和直线l:x=1,P是动点,作PQ⊥l,垂足为Q,且(| PC |
| PQ |
| PC |
| PQ |
(1)求曲线M的方程;
(2)点O是坐标原点,是否存在斜率为1的直线m,使m与M交于A、B两点,且
| CB |
| OA |
分析:(1)先由 (
+2
)(
-2
)=0.得 |
|=2|
|.直接设出点P的坐标,代入整理即可求出点P所在曲线以及曲线的轨迹方程M;
(2)假设存在斜率为1的直线m:y=x+n,将直线的方程代入双曲线的方程,消去y得到关于x的一元二次方程,整理得13年n2-8n+76=0,因其判别式△<0,所以不存在斜率为1的直线m满足题意.
| PQ |
| PC |
| PQ |
| PC |
| PQ |
| PC |
(2)假设存在斜率为1的直线m:y=x+n,将直线的方程代入双曲线的方程,消去y得到关于x的一元二次方程,整理得13年n2-8n+76=0,因其判别式△<0,所以不存在斜率为1的直线m满足题意.
解答:解:(1)由(
+2
)•(
-2
)=0知|
|2-4|
|2=0,∴|
|=2|
|.(2分)
设P(x,y),代入上式得
=2|x-1|,(4分)
平方整理得
-
=1.(6分)
(2)假设存在斜率为1的直线m:y=x+n,使m与M交于A、B两点,与
-
=1.联立,
得2x2-2nx-(n2+12)=0.设A,B的坐标分别为(x1,y1),(x2,y2),
∴x1+x2=n,x1x2=-
,①(8分)
=2
,得(x2-4,y2)=2(x1,y1),∴
,②(9分)
将②代入①得∴
,(10分)
消去x1,整理得n2-8n+76=0,因其判别式△=82-4×13×76<0
所以不存在斜率为1的直线m满足题意.(12分)
| PC |
| PQ |
| PC |
| PQ |
| PC |
| PQ |
| PC |
| PQ |
设P(x,y),代入上式得
| (x-4)2+y2 |
平方整理得
| x2 |
| 4 |
| y2 |
| 12 |
(2)假设存在斜率为1的直线m:y=x+n,使m与M交于A、B两点,与
| x2 |
| 4 |
| y2 |
| 12 |
得2x2-2nx-(n2+12)=0.设A,B的坐标分别为(x1,y1),(x2,y2),
∴x1+x2=n,x1x2=-
| n2+12 |
| 2 |
| CB |
| OA |
|
将②代入①得∴
|
消去x1,整理得n2-8n+76=0,因其判别式△=82-4×13×76<0
所以不存在斜率为1的直线m满足题意.(12分)
点评:本题综合考查了椭圆的定义,直线与抛物线的位置关系以及向量共线问题.是一道综合性很强的好题.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
 P是动点,作
P是动点,作 垂足为Q,且
垂足为Q,且 设P点的轨迹是曲线M。
设P点的轨迹是曲线M。 若存在,求出直线m的方程;若不存在,说明理由。
若存在,求出直线m的方程;若不存在,说明理由。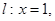 P是动点,作
P是动点,作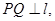 垂足为Q,且
垂足为Q,且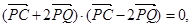 设P点的轨迹是曲线M。
设P点的轨迹是曲线M。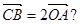 若存在,求出直线m的方程;若不存在,说明理由。
若存在,求出直线m的方程;若不存在,说明理由。