题目内容
(本小题满分12分)
已知点C（4，0）和直线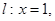
P是动点，作
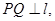垂足为Q，且
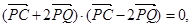设P点的轨迹是曲线M。
（1）求曲线M的方程；
（2）点O是坐标原点，是否存在斜率为1的直线m，使m与M交于A、B两点，且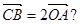
若存在，求出直线m的方程；若不存在，说明理由。
【答案】
解：（1）由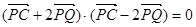
知
，
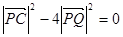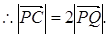……………………（2分）
设P（x，y）,代入上式得
，……………………（4分）
平方整理得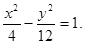
…………………（6分）
（2）假设存在斜率为1的直线m：y=x+n,使m与M交于A、B两点，与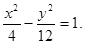联立，得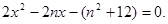
设A，B的坐标分别为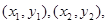
①…………………（8分）
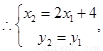② ……………………（9分）
将②代入①得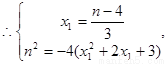
…………………（10分）
消去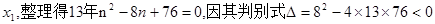
所以不存在斜率为1的直线m满足题意。…………………（12分）
【解析】略
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
