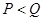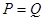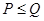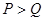题目内容
已知函数f(x)=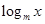 (m为常数0<m<1),且数列{f(
(m为常数0<m<1),且数列{f( )}是首项为2,公差为2的等差数列.
)}是首项为2,公差为2的等差数列.
(1)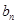 =
= f(
f( ),当m=
),当m=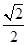 时,求数列{
时,求数列{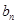 }的前n项和
}的前n项和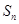 ;
;
(2)设 =
= ·
·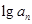 ,如果{
,如果{ }中的每一项恒小于它后面的项,求m的取值范围.
}中的每一项恒小于它后面的项,求m的取值范围.
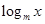 (m为常数0<m<1),且数列{f(
(m为常数0<m<1),且数列{f( )}是首项为2,公差为2的等差数列.
)}是首项为2,公差为2的等差数列.(1)
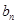 =
= f(
f( ),当m=
),当m=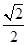 时,求数列{
时,求数列{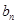 }的前n项和
}的前n项和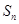 ;
;(2)设
 =
= ·
·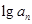 ,如果{
,如果{ }中的每一项恒小于它后面的项,求m的取值范围.
}中的每一项恒小于它后面的项,求m的取值范围.(1)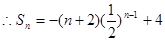
(2)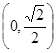
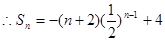
(2)
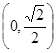
试题分析:解: 因数列
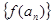 是首项为2,公差为2的等差数列,所以
是首项为2,公差为2的等差数列,所以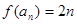
又
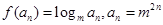 2分
2分 当
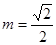 时
时 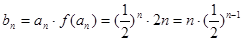 3分
3分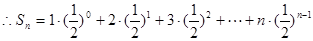

两式相减
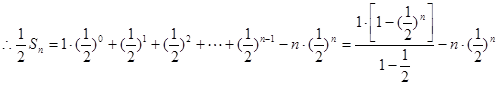
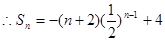 6分
6分由(1)知
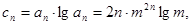 要使
要使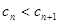 对于一切
对于一切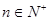 成立,即
成立,即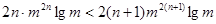 对一切
对一切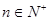 成立
成立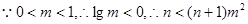 对一切
对一切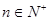 成立 9分
成立 9分只需
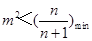 ,而
,而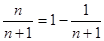 单调递增,
单调递增,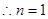 时
时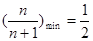
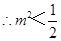 得
得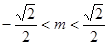
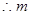 的取值范围是
的取值范围是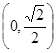 12分
12分点评:主要是考查了数列的求和以及数列的单调性的运用,属于中档题。

练习册系列答案
相关题目
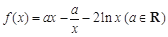 .
.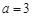 ,求曲线
,求曲线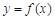 在点
在点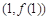 处的切线方程;
处的切线方程;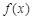 的单调区间;
的单调区间;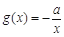 .若至少存在一个
.若至少存在一个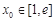 ,使得
,使得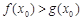 成立,求实数
成立,求实数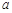 的取值范围.
的取值范围.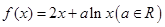 .
.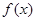 的单调性;
的单调性;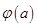 ,求
,求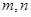 为
为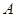 内的任意两个值,试比较
内的任意两个值,试比较 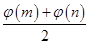 与
与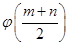 的大小.
的大小.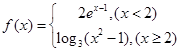 则不等式
则不等式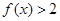 的解集为( )
的解集为( )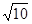 ,+∞)
,+∞)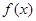 是R上的偶函数,且在
是R上的偶函数,且在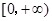 上单调递增,则
上单调递增,则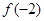 ,
,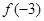 ,
, 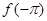 的大小顺序是:( )
的大小顺序是:( )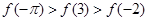
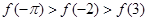
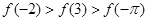
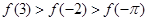
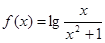 ,有下列结论:①函数
,有下列结论:①函数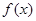 的定义域是(0,+∞);②函数
的定义域是(0,+∞);②函数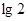 ;④当
;④当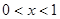 时,函数
时,函数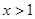 时,函数
时,函数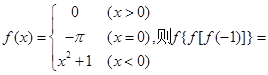
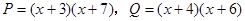 ,则P,Q的大小关系为
,则P,Q的大小关系为