题目内容
已知x=-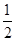 是函数f(x)=ln(x+1)-x+
是函数f(x)=ln(x+1)-x+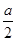 x2的一个极值点。
x2的一个极值点。
(1)求a的值;
(2)求曲线y=f(x)在点(1,f(1))处的切线方程
(1)a=2.(2) y=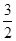 x+ln2-
x+ln2-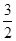 。
。
解析试题分析:(1)先对原函数求导,得到极值点,而极值点是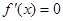 方程的根,最后解方程即可.
方程的根,最后解方程即可.
(2)曲线y=f(x)在点(1,f(1))处的切线的斜率k=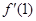 ,再求出f(1),最后可以求出切线方程.
,再求出f(1),最后可以求出切线方程.
(1)f(x)="ln(x+1)-" x+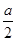 x2,∴f'(x)=
x2,∴f'(x)= -1+ax
-1+ax
由于x=-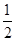 是函数f(x)的一个极值点.∴f'(-
是函数f(x)的一个极值点.∴f'(-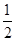 )="0," 即2-1-
)="0," 即2-1-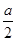 =0,故a=2.
=0,故a=2.
(2)由(1)知:f'(x)= +2x-1 从而曲线y=f(x)在点(1,f(1))处的切线的斜率k=
+2x-1 从而曲线y=f(x)在点(1,f(1))处的切线的斜率k=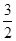 ,又f(1)=ln2,
,又f(1)=ln2,
故曲线y=f(x)在点(1,f(1))处的切线方程为y=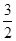 x+ln2-
x+ln2-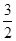 。
。
考点:导数的几何意义;利用导数求切线方程.

练习册系列答案
相关题目
 ex,a,b
ex,a,b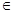 R,且a>0.
R,且a>0.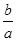 的取值范围.
的取值范围.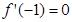 .
.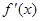 是
是 的导函数,
的导函数,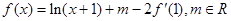 ,且函数
,且函数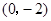 .
.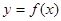 的表达式;
的表达式;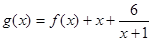 的单调区间和极值.
的单调区间和极值.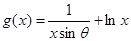 在
在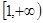 上为增函数,
上为增函数,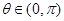 ,
,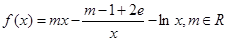
 的值;
的值;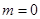 时,求函数
时,求函数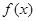 的单调区间和极值;
的单调区间和极值;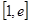 上至少存在一个
上至少存在一个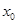 ,使得
,使得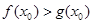 成立,求
成立,求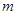 的取值范围.
的取值范围.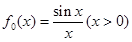 ,设
,设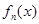 为
为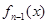 的导数,
的导数,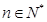
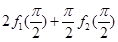 的值;
的值;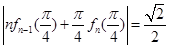 都成立.
都成立.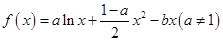 ,曲线
,曲线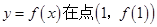 处的切线斜率为0
处的切线斜率为0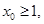 使得
使得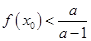 ,求a的取值范围。
,求a的取值范围。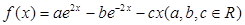 的导函数
的导函数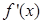 为偶函数,且曲线
为偶函数,且曲线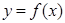 在点
在点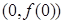 处的切线的斜率为
处的切线的斜率为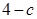 .
.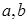 的值;
的值; 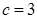 ,判断
,判断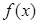 的单调性;
的单调性;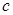 的取值范围.
的取值范围.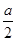 x2.
x2.