题目内容
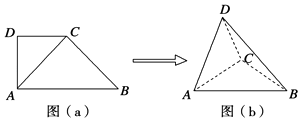
【题目】（本题满分14分）如图，我市有一个健身公园，由一个直径为2km的半圆和一个以
为斜边的等腰直角三角形
构成，其中
为的中点．现准备在公园里建设一条四边形健康跑道
，按实际需要，四边形的两个顶点
分别在线段
上，另外两个顶点
在半圆上， 
，且
间的距离为1km．设四边形
的周长为
km．
（1）若分别为的中点，求
长；
（2）求周长的最大值．
【答案】（1）
（2）
【解析】
试题分析：（1）求
长，就是求圆中弦长，关键求出圆心到弦所在直线距离：因为
分别为
的中点，所以圆心到直线CD距离为半径的一半，即
，又
间的距离为1km，所以圆心到弦所在直线距离为，因此
（2）求四边形
的周长，就是要表示出四边长度，如何取自变量是解决问题的关键，设角是一个较好的方法，如设
，其中M为AB中点，则
，
，
，再根据基本不等式其周长最值
试题解析：（1）解：连结
并延长分别交于
，连结
，
∵分别为的中点，
，∴
，
为等腰直角三角形，
为斜边，
，
．∵
，∴
． 3分
在
中，
，∴
，
∴
． 6分
（2）解法１ 设，
．
在中，，∴
，
．
∵，∴
，
∴
， 8分
∴
10分
，（当
或
时取等号）
∴当
或
时，周长
的最大值为
． 14分
解法２ 以
为原点，
为
轴建立平面直角坐标系．
设
，
，
，
，
∴
，
，
． 8分
∴
10分
，
（当
，
或
，
时取等号）
∴当，或，时，周长的最大值为
． １４分
练习册系列答案
相关题目
【题目】某种产品的广告费用支出x万元与销售额y万元之间有如下的对应数据：
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
（1）画出散点图；
（2）求回归直线方程；
（3）据此估计广告费用为12万元时，销售收入y的值．
