题目内容
关于直线 与平面
与平面 ,有以下四个命题:
,有以下四个命题:
①若 且
且 ,则
,则 ; ②若
; ②若 且
且 ,则
,则 ;
;
③若 且
且 ,则
,则 ; ④若
; ④若 且
且 ,则
,则 ;
;
其中真命题的序号是( )
| A.①② | B.③④ | C.①④ | D.②③ |
D
解析试题分析:由题意,不同的两条直线m,n与两个平面α,β,A,D两个选项可由线线垂直的条件作作出判断,C,B两个选项可由线线平行的条件作出判断,得出正确选项解:由题意两条直线m,n与两个平面α,β由于m∥α,n∥β且α∥β,不能确定两条直线的位置关系,故若m∥α,n∥β且α∥β,则m⊥n是假命题;由于若m⊥α,n⊥β且α⊥β,不能确定两条直线的位置关系,故若m⊥α,n⊥β且α⊥β,则m∥n是假命题;由于m∥α,n⊥β且α⊥β不能确定两条直线的位置关系,故若m∥α,n⊥β且α⊥β,则m∥n是假命题;由于n∥β且α∥β可得出n?α或n∥α,又m⊥α可得出m⊥n故若m⊥α,n∥β且α∥β,则m⊥n是真命题.综上知,D选项正确,故选D
考点:空间中点先面的位置关系
点评:本题的考点是间中直线一直线之间的位置关系,考查了线线平行与线线垂直的条件,解题的关键是理解题意,有着较强的空间立体感知能力,本题考查了空间想像能力,推理判断的能力,是高考中常见题型,其特点是涉及到的知识点多,知识容量大,因此备受高考命题者青睐

在正方体 中,
中, 为体对角线
为体对角线 的三等分点,则
的三等分点,则 到各顶点的距离的不同取值有 ( )
到各顶点的距离的不同取值有 ( )
| A.3个 | B.4个 | C.5个 | D.6个 |
如图,长方体ABCD—A1B1C1D1中,BB1=BC,P为C1D1上一点,则异面直线PB与B1C所成角的大小( )
| A.是45° | B.是60° |
| C.是90° | D.随P点的移动而变化 |
设m,n是不同的直线, 是不同的平面,下列命题中正确的是
是不同的平面,下列命题中正确的是
A.若m// |
B.若m// |
C.若m//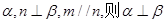 |
D.若m// |
设 是直线,
是直线, ,
, 是两个不同的平面,下列命题正确的是( ).
是两个不同的平面,下列命题正确的是( ).
A.若 , , ,则 ,则 | B.若 , , ,则 ,则 |
C.若 , , ,则 ,则 | D.若 , ,  ,则 ,则 |
若直线上有两个点在平面外,则( )
| A.直线上至少有一个点在平面内 |
| B.直线上有无穷多个点在平面内 |
| C.直线上所有点都在平面外 |
| D.直线上至多有一个点在平面内 |
点 到直线
到直线 :
: 的距离的最大值为( )
的距离的最大值为( )
A. | B. | C. | D. |
平面 和直线
和直线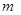 ,给出条件:①
,给出条件:① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ .为使
.为使 ,应选择下面四个选项中的条件( )
,应选择下面四个选项中的条件( )
| A.①⑤ | B.①④ | C.②⑤ | D.③⑤ |
已知直线 ,平面
,平面 ,且
,且 ,给出四个命题: ①若
,给出四个命题: ①若 ∥
∥ ,则
,则 ;②若
;②若 ,则
,则 ∥
∥ ;③若
;③若 ,则
,则 ∥m;④若
∥m;④若 ∥m,则
∥m,则 .其中真命题的个数是
.其中真命题的个数是
| A.4 | B.3 | C.2 | D.1 |